- #1
swirlydragon
- 2
- 0
According to Gauss Law, we only consider charges which are inside the surface to produce net flux.
We disregard the charges outside the surface because they produce zero net flux (as the electric field lines enter the surface and leave the surface producing zero net flux)
My question is, since we don't consider the charges outside the surface to produce flux then why do we consider the electric field of those charges when solving Gauss Law problems?
In the formula, we consider only the charges inside the Gaussian surface but when it comes to electric field, we consider electric field caused by all the charges (whether they be inside or outside the Gaussian surface). Why?
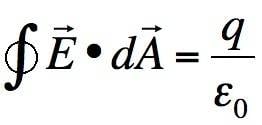
We disregard the charges outside the surface because they produce zero net flux (as the electric field lines enter the surface and leave the surface producing zero net flux)
My question is, since we don't consider the charges outside the surface to produce flux then why do we consider the electric field of those charges when solving Gauss Law problems?
In the formula, we consider only the charges inside the Gaussian surface but when it comes to electric field, we consider electric field caused by all the charges (whether they be inside or outside the Gaussian surface). Why?