- #1
sankalpmittal
- 785
- 15
Homework Statement
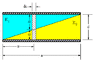
See the image:
http://postimg.org/image/q550yqqd1/
Left click to enlarge...
Homework Equations
For a parallel plate capacitor, Capacitance C=KεoA/d
A is area of plate and d is distance between the two plates..
The Attempt at a Solution
I do not know how to approach. I divided the capacitor along the diagonal into two halves. For the first half,
dC1 = K1εodA/dl
I took a strip of edge dx and length "l" perpendicular to the capacitor. Area of that strip= (x+dx)2-x2=2xdx..
dA=2xdx
Hence,
dC1 = 2K1εoxdx/dl
Now taking an angle θ, tanθ=d/a= (d-l)/(a-x)...
Am I going in the right direction ?
Please help !
Thanks in advance...
Last edited by a moderator: