Why are my integrals giving different results for the same function?

  • Thread starter MartinV05
  • Start date
  • Tags
    Integrals
In summary, the conversation is about a problem with two different integrals in an exercise. The person is confused because both functions are the same but the integrals are different. However, it is pointed out that the two integrals are actually identical due to the absolute value. The final expressions both have a "-" and there is no need to make it go away.
  • #1
MartinV05
23
0
I've been solving this exercise and I came to a point when one function can get two different integrals:
integral.jpg

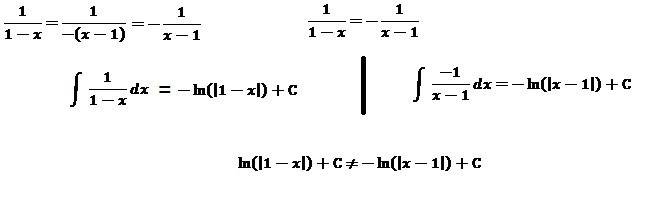
Am I doing something wrong? Because both functions are the same, and the integrals (indefinite) are really different. This is a huge problem, because this is almost the final step of an exercise and when I exchange the current variable (x) with the previously defined function for it, the solution is VERY different.
**There should be a "-" in front of the last line of equation in the picture.
 
Last edited:
Physics news on Phys.org
  • #2
No, the two integrals are NOT "really different"- they are identical. |x- 1|= |1- x| so, of course, -ln(|x-1|)+ C= -ln(|1- x|)+ C.
 
  • #3
Since you are taking the absolute value, |1-x| and |x-1| are the same.
 
  • #4
In the final expression a "-" appears, but I don't see how we can just make it go away (turn positive) when we are working with variables. The variable can be +-∞.
 
  • #5
The final expressions both have a "-". There is no need to make it go away.
 

1. What is an integral?

An integral is a mathematical concept that represents the accumulation of a quantity over an interval. It is essentially the inverse operation of differentiation, and is used to find the total value of a function over a given range.

2. What are the different types of integrals?

There are several types of integrals, including definite integrals, indefinite integrals, improper integrals, and line integrals. Definite integrals have specific bounds and can be evaluated to find a numerical value, while indefinite integrals do not have bounds and are used to find a general solution to a function. Improper integrals deal with infinite limits, and line integrals involve integrating a function along a specific path.

3. How do you solve an integral?

Solving an integral involves using integration techniques such as substitution, integration by parts, or partial fractions. The specific method used depends on the form of the integral and the function being integrated. It is important to also keep track of any constants or limits when solving an integral.

4. What is the importance of integrals in science?

Integrals have many applications in science, particularly in physics and engineering. They are used to find the area under a curve, which is important for calculating quantities such as displacement, velocity, and acceleration. Integrals are also used in the calculation of volumes and mass in three-dimensional space, making them crucial in fields such as fluid mechanics and electromagnetism.

5. Can integrals be solved using software or calculators?

Yes, integrals can be solved using software or calculators. There are many programs and online tools available that can solve integrals numerically or symbolically. However, it is important to understand the concepts and techniques behind integration in order to use these tools effectively and accurately interpret the results.

Similar threads

A Integral of 2 Bessel functions of different orders
    • Calculus
Replies
3
Views
2K
I Why is this closed line integral zero?
    • Calculus
Replies
8
Views
2K
I Convergence of sequences of functions with differing domains?
    • Calculus
Replies
11
Views
1K
I How to evaluate the enclosed area of this implicit curve?
    • Calculus
Replies
2
Views
2K
A Integrating a function of which poles appear on the branch cut
    • Calculus
Replies
1
Views
2K
I Munkres-Analysis on Manifolds: Extended Integrals
    • Calculus
Replies
5
Views
1K
I Why does the answer key sometimes have a different form compared to my solution?
    • Calculus
2
Replies
68
Views
4K
I Spivak's Definition of Integrals vs Stewart's
    • Calculus
Replies
9
Views
3K
I In which sense(s) do square integrable functions go to zero at infinity?
    • Topology and Analysis
Replies
2
Views
142
I Solving this integral equation
    • Calculus
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top