- #1
xenogizmo
- 30
- 0
Hey everybody..
I got this space geometry question that had me stumped.. Please help me out.. Here goes:
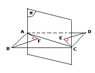
ABCD is a parallelogram. The plane π was drawn passing through the diagonal AC.
If DE was perpendicular to π, BF was perpendicular to π.
Prove that BF = DE
please see the attached drawing
I got this space geometry question that had me stumped.. Please help me out.. Here goes:
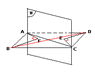
ABCD is a parallelogram. The plane π was drawn passing through the diagonal AC.
If DE was perpendicular to π, BF was perpendicular to π.
Prove that BF = DE
please see the attached drawing