Rank the paths according ∫B.ds around the paths during the discharging of the capacitor

[hidemi]

Homework Statement:

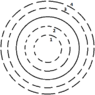
The diagram shows one plate of a parallel-plate capacitor from whin the capacitor. The plate is circular and has radius R. The dashed circles are four integration paths and radii of r1=R/4, r2=R/2, r3=3R/2, and r4=2R. Rank the paths according to the magnitude of ∫B.ds
around the paths during the discharging of the capacitor, least to greatest.

A) 1, 2 and 3 tie, then 4
B) 1,2,3,4
C) 1, then 2 and 4 tie, then 3
D) 4,3,1,2

the answer is C

E) all tie

Relevant Equations:

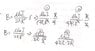
B = μ0*I / 2πr

My calculation is as attached. Where am I wrong?

 

[TSny]

I agree with your results for B. So, it looks like (C) would be the correct answer if the question asked for the ranking of B on each path, rather than asking for the ranking of ∫Bds. None of the answers appear to be correct for the ranking of ∫Bds.

[Edit: For the ranking of ∫Bds, you can argue that one of the answers is correct if you take into account the fringing of the E field of the capacitor.]

 

[Steve4Physics]

... Rank the paths according to the magnitude of ∫B.ds
.
My calculation is as attached. Where am I wrong?

From your working it looks like you have tried to rank the different values of B. But the question specifically says “Rank ... according to the magnitude of ∫B.ds”. You answered the wrong question!

The question is about displacement current. So ideally you shouldn’t use $I$. Use (for example) $I_D$.

(Explanatory note follows, if needed:

Inside of the capacitor is a dielectric (vacuum, or air, or some other insulator). This mean no physical current (moving charge) actually crosses the gap between the plates.

The changing electric flux inside the capacitor generates a magnetic field. $I_D$ is a ‘fictitious’ current which would create the same magnetic field as the changing electric flux. So, when finding the magnetic field, we can ‘pretend’ $I_D$ is actually flowing between the plates like a real current.)

Since the electric field is uniform, $I_D$’s distribution is the same as a uniform current through a cylindrical conductor radius R. The current, $I_r$, through an ‘inner cylinder’ (r≤R) is $I_D \frac {r^2}{R^2}$ because it is proportional to cross-sectional area.

The current, $I_r$, through an ‘outer cylinder’ (r>R) is , $I_r=I_D$, because it is the total current.

Ampere’s law tell us $\int B.ds = \mu_0 I_r$. So we are simply being asked to rank the values of $\mu_0 I_r$ for different value of r.

Once that’s fully understood, no calculations at all are needed to answer the question! What do you think the answer should be?

Unfortunately (as already noted by @TSny) the correct answer is not on the answer-list.

 

[hidemi]

Thank you so much.

 

[hidemi]

I agree with your results for B. So, it looks like (C) would be the correct answer if the question asked for the ranking of B on each path, rather than asking for the ranking of ∫Bds. None of the answers appear to be correct for the ranking of ∫Bds.

[Edit: For the ranking of ∫Bds, you can argue that one of the answers is correct if you take into account the fringing of the E field of the capacitor.]

Thank so much.

 

[Delta2]

The correct answer for the ranking of the magnitude (absolute value) of $\int \mathbf{B}\cdot d\mathbf{s}$ (and not for the ranking of B as your work is) is 1<2<3=4.

 

[hidemi]

The correct answer for the ranking of the magnitude (absolute value) of $\int \mathbf{B}\cdot d\mathbf{s}$ (and not for the ranking of B as your work is) is 1<2<3=4.

Yes I agree with you, thanks for commenting!