How Does the Reciprocal Lattice Relate to Real Space Lattice Vectors?

[nixego]

Hey folks,

Here's my problem:

Knowing that for reciprocal lattice vectors K and real space lattice vectors R:

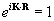
and using the Kronecker delta:

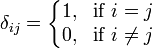
I need to prove b₁, b₁, b₃ as shown http://www.doitpoms.ac.uk/tlplib/brillouin_zones/reciprocal.php" :

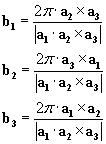
I understand that for the first equation above, the exponential needs to equal zero for the expression to equal 1. So I have K.R=0 as one piece of information, but I don't see how this leads me to the expressions for b₁, b₁, b₃ which I'm trying to find.

I'm assuming this is part of the proof:

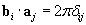
But how do I use this and where does the 2*pi come from?


Thanks all!

 

[jensa]

This type of calculation can be found in any book on solid-state physics.

Anyway:
So we know that $\mb{R}=\sum_i n_i\mb{a}_i, \ n_i\in \mathbb{Z}$, and we want to find a basis $\mb{b}_i$ of our reciprocal lattice such that for $\mb{K}=\sum_i m_i\mb{b}_i, \ m_i\in \mathbb{Z}$ we have $\mb{K}\cdot\mb{R}=2\pi l, \ l\in \mathbb{Z}$, which means $e^{iK\cdot R}=1$. It is quite easy to see that this is satisfied if $a_i\cdot b_j=2\pi \delta_{ij}$. Problem is just to find $b_i$ which satisfy this condition. A vector $a_1\times a_2$ will be orthogonal to both $a_1$ and $a_2$ so it makes sense to define $$b_3 \propto a_1\times a_2$$ since it will naturally give you $a_i\cdot b_3\propto \delta_{i3}$ and so on. The rest is just a matter of finding the correct normalization, which I leave to you.

 

[charng]

Hi there,

The proof you are trying to show is the relationship between the reciprocal lattice vectors and the real space lattice vectors. To understand this relationship, we need to first understand the concept of reciprocal lattice.

Reciprocal lattice is a mathematical construct that is used to describe the periodicity of a crystal in reciprocal space. It is defined as the set of all wave vectors that can be diffracted by the crystal. The reciprocal lattice vectors are perpendicular to the real space lattice vectors and are defined as:

b1 = 2*pi*(a2*a3)/(a1*(a2 x a3))
b2 = 2*pi*(a3*a1)/(a2*(a3 x a1))
b3 = 2*pi*(a1*a2)/(a3*(a1 x a2))

where a1, a2, and a3 are the real space lattice vectors.

Now, let's look at the first equation you mentioned:

K.R = 0

This equation tells us that the dot product of the reciprocal lattice vector K with the real space lattice vector R is equal to zero. This means that K and R are perpendicular to each other, which is true for all reciprocal lattice vectors.

Next, we can use the Kronecker delta to rewrite this equation as:

K.R = δij, where δij is the Kronecker delta function.

Now, if we substitute the expressions for b1, b2, and b3 into this equation, we get:

2*pi*(a2*a3)/(a1*(a2 x a3)) * R = δij

This equation can be rewritten as:

2*pi*(a2*a3)/(a1*(a2 x a3)) * (a1*i + a2*j + a3*k) = δij

where i, j, and k are the unit vectors along the x, y, and z directions, respectively.

Now, if we consider the dot product of the reciprocal lattice vector b1 with the real space lattice vector a1, we get:

b1.a1 = 2*pi*(a2*a3)/(a1*(a2 x a3)) * (a1*i + a2*j + a3*k) . a1

= 2*pi*(a2*a3)/(a1*(a2 x a3)) * (a1*a1) = 2*pi

Similarly, we can show that b2