- #1
The_Prime_Number
- 3
- 0
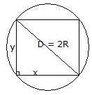
The problem asks me to show that the maximum possible area for a rectangle
inscribed in a circle of radius R is 2R^2. It also gives a hint saying that I should first maximize the square of the area.
I set the problem up as xy = 2R^2. I decided to work on the left side and wrote it as x(2R). But, I don't know where to go from here. Thanks.
inscribed in a circle of radius R is 2R^2. It also gives a hint saying that I should first maximize the square of the area.
I set the problem up as xy = 2R^2. I decided to work on the left side and wrote it as x(2R). But, I don't know where to go from here. Thanks.