Reflected Light at 3D Angle: Shift in Polarization

[lvb884]

I've searched high and low for answers to this, and a friend of mine finally pointed me in the right direction. I decided to write a post about it so hopefully others who have the same question will find the answer more easily.

When linearly polarized light is reflected at a 3D angle, the polarization angle rotates with respect to the original frame of reference. The reflected image also rotates.

The reason for this is because light doesn't care about what frame of reference you're in. It only cares about the orientation of the mirror it's reflecting from.

For example, if I'm using a periscope to look at something in front of me, such that the light beam stays in the same 2D plane, the polarization and image will not change. Here's a handy picture that illustrates this:

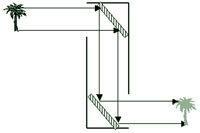
If the second mirror is rotated 90 deg, then the polarization (and image) will rotate 90 deg. If our frame of reference is the ground or some other horizontal surface, this means that s-polarized light can be converted to p-polarized light and vice versa. Here's another handy picture:

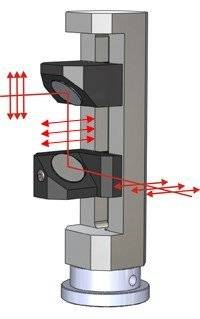
If the second mirror is rotated at an arbitrary angle between 0 and 90 deg, guess what? The polarization angle of the reflected beam will also be somewhere between 0 and 90 deg.

You don't even need two mirrors to do this. In both cases above, the rotation axis for each mirror was perpendicular to the light beam. Instead, you could use only one mirror with an arbitrary rotation axis in 3D space, and you could still rotate the polarization to any angle you want.

So how do you figure out what the output polarization angle would be? Just do a bunch of cross products and some trigonometry. That's pretty much it.

Steve Scott and Jinseok Ko from MIT wrote up a nice pedagogical explanation for how to determine the polarization shift for light reflected from a flat mirror. I've attached it as a PDF. You can access the online file here: http://www-internal.psfc.mit.edu/~sscott/MSEmemos/mse_memo_83c.pdf

Basically, you start with cartesian coordinates representing your desired frame of reference (e.g., optics table), and then create a separate set of coordinates that uses the mirror as the frame of reference. After you calculate the reflected polarization angle, just convert the vector coordinates back into your desired frame of reference. In the attached file, Scott and Ko use an angle beta for the offset between the x (or y) axis in the original space and the vector corresponding to s-polarized light (or p-polarized light) for the mirror surface. They explain it very well, so I won't bother rephrasing.

Note that in the attached explanation, all polarization angles are right-handed, where each angle is measured as a counterclockwise rotation with the k-vector pointed toward you. This means that for an ideal metallic mirror, the reflected polarization angle is reversed (negative) compared to the incident angle.

Also note that the attached explanation assumes you already know the orientation of the incident k-vector with respect to the mirror plane. If you do not know the orientation of the mirror but you do know the angle of the reflected k-vector with respect to the incident, then you can easily determine the normal vector of the mirror by calculating the midpoint between the two k-vectors. From there, you can rotate all three vectors so the mirror normal is in the xz-plane and the incident k-vector is in the xy-plane. (This can be done with basic rotation matrices: https://en.wikipedia.org/wiki/Rotation_matrix.) Then, to determine the reflected polarization angle, you can follow the approach given by Scott and Ko for a tilted mirror (see equation 18, attached).

And I would like to point out that, especially if you're doing this in Matlab, it's more accurate to use cross products than trig identities whenever possible because then you will preserve the direction of rotation for the polarization angle.

Enjoy!

 

[eljose79]

Thank you for sharing your findings on the rotation of polarization angle in reflected light. I find this topic very interesting and would like to add some additional information.

Firstly, the effect of polarization rotation in reflected light is not limited to just mirrors. It can also occur in other surfaces, such as glass or water, depending on the angle of incidence and the refractive index of the material.

Secondly, the rotation of polarization angle can also be influenced by the presence of a magnetic field. This is known as the Faraday effect and is often used in devices such as optical isolators and modulators.

Lastly, as you mentioned, cross products are indeed a more accurate way to calculate the rotation of polarization angle. This is because they take into account the direction of rotation, which is important in cases where the angle of incidence is not perpendicular to the surface.

Thank you for promoting a discussion on this topic and for providing a helpful resource for those interested in learning more about it.