- #1
brycenrg
- 95
- 2
Homework Statement
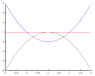
Consider the graph y = e^x
Homework Equations
Make an equation that results in reflecting about the line y = 2
The Attempt at a Solution
I came up with 2 - e^x
And when I put it in my calculator it makes sense.
Just -e^x is reflected among y = 0
so if you bring it up 2, to y = 2 then it will be reflected among y = 2.
My webassign says I am incorrect and its actually 4 - e^x, why is this? I don't understand the logic