- #1
dekoi
100 mL of water at 288 K is placed in the freezer compartment of a refrigerator with a coefficient of performance of 4.0. How much heat energy is exhausted into the room as the water is changed to ice at 258 K?
(The answer is 5.34 x 10^4 J)
I tried using the Brayton-cycle refrigerator to understand this problem.
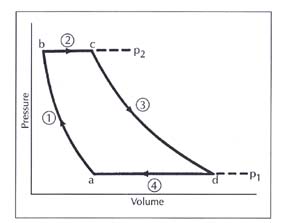
I am assuming that the lower isobar is the part of the graph that I need to analyze, where the low-temperature heat exchanger warms the gas and cools the refrigerator. With this method, I know that [tex]Q = nC_v\Delta T[/tex]. However, I cannot think of a way to find the number of moles (n).
I also don't know if my reasoning is correct (that is, only using the lower isobar of the graph to answer my question).
I am also assuming that my lower temperature (258 K) is equivalent to Tc, and my higher temperature (288 K) is equivalent to Th.
I am not sure if this is correct, however.
I have realized that I need to use work (in) to answer the question, because K = Q / W.
However, the work for an isobar is W = pV, and I do not know the pressure, and am unable to find it since I do not know the number of moles.
Any advice will be greatly appreciated, thank you.
(The answer is 5.34 x 10^4 J)
I tried using the Brayton-cycle refrigerator to understand this problem.
I am assuming that the lower isobar is the part of the graph that I need to analyze, where the low-temperature heat exchanger warms the gas and cools the refrigerator. With this method, I know that [tex]Q = nC_v\Delta T[/tex]. However, I cannot think of a way to find the number of moles (n).
I also don't know if my reasoning is correct (that is, only using the lower isobar of the graph to answer my question).
I am also assuming that my lower temperature (258 K) is equivalent to Tc, and my higher temperature (288 K) is equivalent to Th.
I am not sure if this is correct, however.
I have realized that I need to use work (in) to answer the question, because K = Q / W.
However, the work for an isobar is W = pV, and I do not know the pressure, and am unable to find it since I do not know the number of moles.
Any advice will be greatly appreciated, thank you.