- #1
heman
- 361
- 0
Hi,,
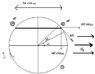
A small circular loop of radius a and Resistance R is kept Coplanar and concentric with a large circular loop of radius b,a<<b.The large loop is kept fixed in space and a constant current I is sent through it.Now the small loop is rotated with a constant velocity w about a diameter.Neglecting the effect of back emf on the current in the small loop find the external torque required on the small loop to keep it in rotation...
Pls help me to how to go for this Problem...I will be grateful for urs Help..
Regards
Heman
A small circular loop of radius a and Resistance R is kept Coplanar and concentric with a large circular loop of radius b,a<<b.The large loop is kept fixed in space and a constant current I is sent through it.Now the small loop is rotated with a constant velocity w about a diameter.Neglecting the effect of back emf on the current in the small loop find the external torque required on the small loop to keep it in rotation...
Pls help me to how to go for this Problem...I will be grateful for urs Help..
Regards
Heman