- #1
mmg0789
- 39
- 0
Homework Statement
Long flights at midlatitudes in the Northern Hemisphere encounter the jet stream, an eastward airflow that can affect a plane's speed relative to Earth's surface. If a pilot maintains a certain speed relative to the air (the plane's airspeed), the speed relative to the surface (the plane's ground speed) is more when the flight is in the direction of the jet stream and less when the flight is opposite the jet stream. Suppose a round-trip flight is scheduled between two cities separated by 3600 km, with the outgoing flight in the direction of the jet stream and the return flight opposite it. The airline computer advises an airspeed of 810 km/h, for which the difference in flight times for the outgoing and return flights is 63 min. What jet-stream speed (in km/h) is the computer using?
Homework Equations
im thinking (x-x0) = 1/2(v0 + v)t
maybe
The Attempt at a Solution
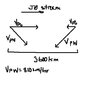
attached is a picture of what i think this scenario looks like,
i found Vpg for the plane going to be cos(theta)/810
but I am not really sure what else to do