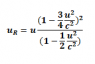Relativistic relative velocity of particles

[scottJH]

Homework Statement

In a given inertial frame two particles are shot out simultaneously from a given point with equal speeds u at an angle of 60 degrees with respect to each other. Using the concept of 4-velocity or otherwise, show that the relative speed of the particles is given by

$u_R = u(1-3u^2/4c^2)/(1-u^2/2c^2)$

I have tried this a number of ways but always end up getting

$u_R = u(1-3u^2/4c^2)$

So I guess my question is which answer is correct?

Homework Equations

$u'_x = (ux-v)/(1-v*ux/c^2)$ and $u'_y = uy/\gamma(1-v*ux/c^2)$

The Attempt at a Solution

[/B]
I set S' as the stationary state of particle A, moving at a velocity u in the x direction. This meant that particle A was at rest in this frame. Therefore the velocity of B in the S' frame is the relative velocity of the two particles.

For particle B I obtained:

$u'_x = -u/2$ and $u'_y = usin60/\gamma$

Then using those values calculated the relative velocity to be

$u_R = u(1-3u^2/4c^2)$I apologise for the layout of the equations because it is my first time posting.

 

[PeroK]

You got off on the wrong foot. You need to work out the velocity of particle B in the initial frame, where the angle is valid.

Also, should the answer you're given have ##2c^2# in the denominator?

 

[TSny]

Hello, and welcome to PF!

Homework Statement

show that the relative speed of the particles is given by

$u_R = u(1-3u^2/4c^2)/(1-u^2/c^2)$

I believe there is a misprint in this expression. Should the expression in parentheses in the numerator be raised to the 1/2 power?

Homework Equations

$u'_x = (ux-v)/(1-v*ux/c^2)$ and $u'_y = uy/\gamma(1-v*ux/c^2)$

The Attempt at a Solution

[/B]
I set S' as the stationary state of particle A, moving at a velocity u in the x direction. This meant that particle A was at rest in this frame. Therefore the velocity of B in the S' frame is the relative velocity of the two particles.

For particle B I obtained:

$u'_x = -u/2$ and $u'_y = usin60/\gamma$

I do not get these results using your relevant equations. In particular, what happened to the denominators of $u'_x$ and $u'_y$?

 

[scottJH]

Hello, and welcome to PF!I believe there is a misprint in this expression. Should the expression in parentheses in the numerator be raised to the 1/2 power?

You are correct, the parentheses should be raised to the 1/2 power.

I do not get these results using your relevant equations. In particular, what happened to the denominators of $u'_x$ and $u'_y$?

For particle B I set the velocity in the x-direction to be $ucos60$ and in the y-direction to be $usin60$. I then just substituted those values into the equations for u'_x and u'_y. I obtained those values for u'_x and u'_y because both u_x and u_y are zero since the we are considering the rest frame of particle A.

 

[scottJH]

You got off on the wrong foot. You need to work out the velocity of particle B in the initial frame, where the angle is valid.

Also, should the answer you're given have ##2c^2# in the denominator?

Is the angle still not valid if we consider the frame where particle A is stationary? Surely the relative velocity of particle B in that frame it the overall relative velocity?

 

[PeroK]

No. You need to use the velocity transformation formula, which is more than just $\gamma$ factor.

 

[TSny]

For particle B I set the velocity in the x-direction to be $ucos60$ and in the y-direction to be $usin60$. I then just substituted those values into the equations for u'_x and u'_y. I obtained those values for u'_x and u'_y because both u_x and u_y are zero since the we are considering the rest frame of particle A.

u_x and u_y are the x and y components of the velocity of B in the original unprimed frame.

 

[scottJH]

Thanks for all your help. I managed to solve it.