Representing a complex oscillating system

[alaspina]

Hello,

I have an equation relating the angular acceleration (d²Θ/dt²) of an undamped system to a forcing function and the an angular term (Θ). The system in question is an inverted pendulum. I know that such an oscillating system can be represented by the following function:

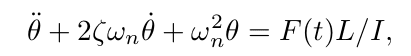
The problem is that in the derivation, some of the terms in F(t) and L are coupled. This means that finding zeta, and omega n (the natural frequency) is not straightforward as I would have to rewrite the equation. My question is, if I solve the coupled function I have now for angular acceleration and angular displacement, then match the curve to the function above where zeta is 0 (undamped), can I then use the coefficients I have found to rewrite my system with the equation above and determine how it acts under different zeta values?

I'll rewrite this in terms of a step by step procedure;1) I have a function (not the one above) that relates angular acceleration to angular displacement and a forcing function. This function DOES NOT have an angular velocity term

2) I want to derive natural frequency from the function; the problem is that unlike the equation above, F(t), the forcing function is not multiplied by the factor L/I (where I is the natural frequency and L is a moment arm length)

3) I solve my function over a given time step for angular acceleration and displacement, and then match my solution to one that matches that of the above function for given values of omega n (I already know what the L and I should be)

4) Will it be mathematically correct to then represent the system with the damping term using the given omega n value I have found from matching the two solutions?

 

[Navin A S]

I hope this makes sense, thanks for any help.Yes, it is mathematically correct to use the omega n value you have found from matching the two solutions to represent the system with the damping term. This is because the omega n value is an intrinsic property of the system that does not change with damping. You can then use this value to calculate the damping coefficient (zeta) from the equation given above. The damping coefficient will then be used to determine the response of the system to the external forcing function.