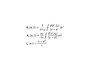Retarded potential in a circle

[mefisto666]

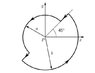
there's a wire shaped as a circular loop that carries a current I=ct. half the loop has radius A and at 45 degrees the radius of the second half of the loop changes to b. Find the retarded potentials V(t) and A(t)



The way i thought of approaching this is by dividing the loop into two sections and calculating the retarded potentials separately for each half of the circle. So, I would have two integrals of the form dl, and each integral would have the limits of integration associated with each part of the loop my only concern is that is one single wire, so I don't know if my initial approach would be correct.

any help appreciated thanks.

 

[gabbagabbahey]

Hi mefisto666, welcome to PF!

Your problem description isn't 100% clear to me...could you provide a sketch of the wire loop? (Also, in the future, please use the homework help template...when you signed up for your account, this was one of the forum rules you agreed to!)

Anyways, your approach seems fine to me...why would treating each section of the loop separately cause any problems?

What do you get when you apply this approach?

 

[mefisto666]

thanks for the reply gabba. I uploaded a picture, and I thought I did use the template provided. maybe part c was the one I didnt do.

I haven't plugged anything in, but I was thinking using V1-V2 = int(dl) - int(dl), however, since I only have half of the circle, should my limits of integrate for d(phi) be from 0 to pi and not 2pi?

my problem with doing this is that I've only seen this approach when having two radii for let's say to spherical shells close to each other.

 

[gabbagabbahey]

I thought I did use the template provided. maybe part c was the one I didnt do.

Homework questions are supposed to be formatted like in this thread (more or less), and most importantly you are supposed to include any relevant equations.

I haven't plugged anything in, but I was thinking using V1-V2 = int(dl) - int(dl), however, since I only have half of the circle, should my limits of integrate for d(phi) be from 0 to pi and not 2pi?

I'm not sure what you mean by this... what are the general equations for the retarded potentials? You will need to integrate over the entire current distribution either piece by piece or all at once (including the two straight line segments).

 

[mefisto666]

I don't know how to enter formulas so I'm posting an image of the formulas. so, I pretty much need to find phi and A, for the configuration in the previous picture of the wire carrying a uniform current I=ct

 

[gabbagabbahey]

Those are the formulas for the advanced potentials... the retarded potentials are given by:

$$\Phi_r(\textbf{r},t)=\frac{1}{4\pi\epsilon_0}\int \frac{\rho(\textbf{r}',t_r)}{|\textbf{r}-\textbf{r}'|}d\tau'$$

$$\textbf{A}_r(\textbf{r},t)=\frac{\mu_0}{4\pi}\int \frac{\textbf{J}(\textbf{r}',t_r)}{|\textbf{r}-\textbf{r}'|}d\tau'$$

$$t_r\equiv t-\frac{|\textbf{r}-\textbf{r}'|}{c}$$

This forum supports $\LaTeX$ (which is what I used to render the above equations)...you can find a good intro in this thread and you can always click on the images to see the code that generated them.

Anyways, what is $\rho$ in this case?... How about $\textbf{J}$?

 

[mefisto666]

oops, sorry i didn't notice the plus sign for the definition of the retarded potential. I've been deprived of coffee until now, so now I'm thinking more clearly. the problem states that the wire is neutral, so when calculating V, we don't need to worry about what the charge density Rho is since the potential will be zero for a neutral wire, and thus v=0. (right?)

Now, as far as A is concerned, the current density J = $$It_{r}$$ => $$I(t- R/c)$$
*note R=|r-r'|after plugging into the equation for the vector potential A and working it out I have arrived at the next expression

$$\frac{\mu_{0} k}{4\pi} ( t\int\frac{\,dl}{R} +\frac{1}{c} \int\,dl)$$

Now I'm stuck. I think the next step would be to separate the first integral by braking the 1/R into the two different radii, 1/a and 1/b

$$\frac{\mu_{0} k}{4\pi} [ t(\frac{1}{a}\int\,dl + \frac{1}{b}\int\,dl)+\frac{1}{c} \int dl]$$

.but even if I do that, i don't know what to do next. and thanks for all your help, I truly appreciate it

 

[gabbagabbahey]

oops, sorry i didn't notice the plus sign for the definition of the retarded potential. I've been deprived of coffee until now, so now I'm thinking more clearly.

So you are claiming that a lack of coffee caused you to violate causality?

the problem states that the wire is neutral, so when calculating V, we don't need to worry about what the charge density Rho is since the potential will be zero for a neutral wire, and thus v=0. (right?)

Yup.

Now, as far as A is concerned, the current density J = $$It_{r}$$ => $$I(t- R/c)$$
*note R=|r-r'|

You should be careful when making claims like this. $\textbf{J}$ is a current density and a vector, it has units of current divided by area. You can find an expression for it it terms of $I$ and some dirac delta functions though...

after plugging into the equation for the vector potential A and working it out I have arrived at the next expression

$$\frac{\mu_{0} k}{4\pi} ( t\int\frac{\,dl}{R} +\frac{1}{c} \int\,dl)$$

Oh, and what direction does this point in?

 

[mefisto666]

Direction? you lost me there :|

 

[gabbagabbahey]

Both $\textbf{J}$ and $\textbf{A}$ are vectors they have both magnitude and direction.

 

[mefisto666]

True true. According to the book, J(r', t) =I(t) so I will have the direction of J, and that will make A have the same direction. So, shouldn't the direction just be X in this case?

 

[gabbagabbahey]

True true. According to the book, J(r', t) =I(t)

Really?!...Your textbook equates two quantities with different units like this? I'd have to see it to believe it!

So, shouldn't the direction just be X in this case?

The current flows in different directions depending on which section of the wire you are looking at...

 

[mefisto666]

It's griffith...what can I say? and he doesn't just equates them both, he somewhat vaguely shows the reason why you can do this. but forgetting that...I'm still stuck as to where to what to do now.

 

[gabbagabbahey]

I have that text...what section of the text are you referring to here?

Anyways, you have 4 sections of current carrying wire (two straight and two curved)...Let's start with the curved section of radius $b$..which direction (you may as well use cylindrical coordinates $\{s,\phi,z\}$) does the current flow in that section?

 

[mefisto666]

If you have griffith, look at problem 10.10, page 427, sec. 10.2...it doesn't seem like we have to actually have to worry about the straight pieces. and if we use cylindrycal, then I moves in the phi direction.

 

[gabbagabbahey]

If you have griffith, look at problem 10.10, page 427, sec. 10.2...it doesn't seem like we have to actually have to worry about the straight pieces. and if we use cylindrycal, then I moves in the phi direction.

You always have to consider every piece of current and charge...it just so happens that due to symmetry, the contributions to the vector potential of the two straight pieces cancel each other out at the center in that problem...things need not be the same for your problem.

Anyways, yes the current in the curved section moves in the [tex]\hat{\mathbf{\phi}}[/itex] direction. Now, given that the current density is defined as

$$\textbf{J}\equiv \frac{d\textbf{I}}{da_{\perp}}$$ (equation 5.25)

It should be clear that it will be zero everywhere except along the wire; and since the wire has zero extend perpendicular to itself, $\textbf{J}$ must be infinite along the wire. Yet, it must produce a finite result $$I(t)\hat{\mathbf{\phi}}$$ when integrated over the directions perpendicular to the wire...hence the need for Dirac delta functions.

So looking at the same curved section of wire, you see that it has zero extent (width) in both the radial and axial direction and hence you should expect to see a current density of the form

$$\textbf{J}\propto I\delta(s-b)\delta(z)\hat{\mathbf{\phi}}$$

for $-\frac{\pi}{4}\leq\phi\leq \frac{\pi}{4}$ and zero elsewhere (due to just the curved section of radius $b$)

Right?

Now use equation 5.28 to find the proportionality constant and then use a similar method to find $\textbf{J}$ due to each of the other 3 sections.

 

[mefisto666]

ok, I got most of it, but what is "s" inside the delta function? so we get something like this

$$\frac{\mu_{0} }{4\pi} \int \frac{I\delta(s-b)\delta(z)\hat{\mathbf{\phi}}}{R} \.d\phi + \frac{\mu_{0} }{4\pi} \int \frac{I\delta(s-a)\delta(z)\hat{\mathbf{\phi}}}{R} \.d\phi$$

and the limits of integration are
$-\frac{\pi}{4} to \frac{\pi}{4}$ for the first integral and $\frac{\pi}{4} to -\frac{\pi}{4}$ for the second

 

[gabbagabbahey]

$s$ is the distance from the $z$-axis (same as Griffiths' uses)

And what about the two straight line segments?

Also, why are you only integrating over $\phi$ in your expression for $\textbf{A}$...what was your result for the constant of proportionality for $\textbf{J}$?

 

[mefisto666]

I want to attack the curved sections first. so after integrating those two delta functions, I will have half the terms for the A potential?

 

[gabbagabbahey]

Sure, but your integrals look a little off...what was you final expression for $\textbf{J}$ fo the first curved piece?

 

[mefisto666]

ok..scratch everything out. I just e-mailed my prof. and he said that we don't need to use delta function and to only use $$\int \.dl$$ for the path from beginning to end. *dl is a vector

 

[gabbagabbahey]

The idea I'm trying to convey here, is how $\int\textbf{J}d\tau$ is equivalent to $\int Id\textbf{l}$... I think it is worth your while to continue with the delta functions and see for yourself why the two expressions are equivalent for line current distributions.