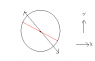- #1
Niles
- 1,866
- 0
Hi
Say I have a linearly polarized optical field traveling along z given by
[tex]
E(z, t) = E(\cos(kz-\omega t)\hat x + \cos(kz-\omega t)\hat y)
[/tex]
In other words, it lies in the 1st and 3rd quadrant. Now the wave passes through a half wave-plate at an angle of 45 degrees (the wave-plate is along y pointing upwards), so the wave becomes
[tex]
E(z, t) = E(\cos(kz-\omega t)\hat x - \cos(kz-\omega t)\hat y)
[/tex]
In other words, it now lies in the 2nd and 4th quadrant. Now I let is pass through a second half wave-plate as shown in the attachment (the red line is the fast axis of the retarder, and the black line is the optical field). Say the angle between the fast axis of the retarder and the polarization of the field is some Ω.
Now I know that after passing through the retarder, the polarization attains an angle of 2Ω besides the 45 degrees from the y-axis. There is two obvious ways for me to represent this:
1) I can do it in terms of a new coordinate system spanned by the axes parallel and perpendicular to the fast axis of the retarder.
2) Use the same "old" coordinate system as with the first retarder
Say I go with #2. What is the easiest way to do this? The only way I see how to do it is to do #1 first, but it seems quite tedious.Niles.
Say I have a linearly polarized optical field traveling along z given by
[tex]
E(z, t) = E(\cos(kz-\omega t)\hat x + \cos(kz-\omega t)\hat y)
[/tex]
In other words, it lies in the 1st and 3rd quadrant. Now the wave passes through a half wave-plate at an angle of 45 degrees (the wave-plate is along y pointing upwards), so the wave becomes
[tex]
E(z, t) = E(\cos(kz-\omega t)\hat x - \cos(kz-\omega t)\hat y)
[/tex]
In other words, it now lies in the 2nd and 4th quadrant. Now I let is pass through a second half wave-plate as shown in the attachment (the red line is the fast axis of the retarder, and the black line is the optical field). Say the angle between the fast axis of the retarder and the polarization of the field is some Ω.
Now I know that after passing through the retarder, the polarization attains an angle of 2Ω besides the 45 degrees from the y-axis. There is two obvious ways for me to represent this:
1) I can do it in terms of a new coordinate system spanned by the axes parallel and perpendicular to the fast axis of the retarder.
2) Use the same "old" coordinate system as with the first retarder
Say I go with #2. What is the easiest way to do this? The only way I see how to do it is to do #1 first, but it seems quite tedious.Niles.
Attachments
Last edited: