What is the Maximum Load W1 That a Supported Beam Can Hold?

[blieveucanfly]

Homework Statement

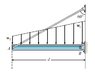
As shown, a uniform beam of length l = 5.90 and 48.2 lb is attached to a wall with a pin at point B. A cable attached at point A supports the beam. The beam supports a distributed weight = 21.0 lb/ft. If the support cable can sustain a maximum tension of 300 lb , what is the maximum value for W₁ ? Under this maximum weight, what is F_By , the vertical component of the support's reaction force at point B?

Homework Equations

$\Sigma$ F = 0
$\Sigma$ M = 0

The Attempt at a Solution

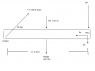
I began by trying to draw a free-body diagram with everything I know put in place. I then came up with 3 equations: The sum of x-axis forces, the sum of y-axis forces, and the sum of moments at point B.

(1) $\Sigma$F_x: 300 cos(60^o)+ B_x= 0
(2) $\Sigma$F_y: 300 sin(60^o)- 48.2 - 123.9 - W₁ - B_y= 0
(3)( this is my problem equation)$\Sigma$M: -300cos(60^o )(5.9ft) - (127.1)(2.95) - W₁(0) - B_y(0) = 0

The problem I can't quite figure out is that if the unknowns F_By and W₁ are applied at B, they create no moments, and that equation becomes useless for solving my system. So, I'm left with an indeterminate system of 2 equations and 3 unknowns. I've attached the Figure referenced in the problem statement and a MS Paint version of my FBD. I just need a nudge in the right direction I think.

I also replaced the distributed load with an equivalent Force of 123.9 lb directed at the center of the beam.

Addendum: I also tried with B_y oriented upward, AND I tried maybe summing the moments at A instead. I still get an indeterminate answer.
Thank you in advance for your help

 

[SteamKing]

You have errors in your calculations:

1. In equation 1, the term 300 cos (60) represents the vertical component of the line tension, not the horizontal. The location of the angle makes a difference in when to use sin/cos for the horiz/vert component calculation. Likewise, your horizontal line component needs correction in your equation 2.

2. w1 and w2 are not concentrated forces, but instead represent distributed loads in lbs/ft. Thus in your moment equation 3) the moment of w1 which you have written is incorrect. Given that w2 = 21 lbs/ft, the problem is asking you to calculate how large w1 can be in lbs/ft such that the tension in the line does not exceed 300 lbs. Given that w2 = 21 lbs/ft, the load on the beam is:
21*5.9 = 123.9 lbs PLUS (w1 - 21)*5.9.
Thus, your equation 2 needs correction.

3. The moment of the distributed load uses 127.1*2.95 instead of 123.9*2.95

4. Likewise, an additional moment term is required for the triangular distributed load which has a value of (w1 - 21) lbs/ft at the wall.

Make these corrections and see if you can solve for w1.

 

[blieveucanfly]

So am I then treating W2 and a rectangular load and w1 as the remaining triangular portion in the diagram? I suppose that would produce two equivalent loads in the middle of the bridge (W1eq and W2eq) which would give me a W1 moment term to solve for)

Thank you so much for your help. I did the (in hindsight) dumbest thing possible by trying to take Statics as a 5-week summer course. 5 chapters in 12 days with no lecture.

I really appreciate your assistance!

Cheers

 

[SteamKing]

Yes. In order to avoid confusion, most texts use capital letters like W and P to denote concentrated loads. For distributed loads, lower case letters are used, which in this case would be w1 and w2.

 

[blieveucanfly]

You have errors in your calculations:
Given that w2 = 21 lbs/ft, the load on the beam is:
21*5.9 = 123.9 lbs PLUS (w1 - 21)*5.9.
Thus, your equation 2 needs correction.

That makes it seem like w2 is completely canceled out by w1

 

[SteamKing]

The trapezoidal load distribution is 21 lbs/ft at the left end of the beam and w1 lbs/ft at the right end. Presumably w1 > w2, therefore w2 + x = w1. x = w1 - w2, where x represents the amount by which w1 is greater than w2.

The trapezoidal distributed load can be split into a constant load distribution plus a triangular load distribution. The constant load distribution is w2 over the length of the beam, and the triangular load distribution is 0 at the LH end of the beam and w1 - w2 at the RH side of the beam. The center of the constant distribution is L/2 from the RH end of the beam and the triangular distribution has a center L/3 from the RH end.

In looking over your moment equation again, I think you forgot to add in the moment due to the weight of the beam, or 48.2 * 2.95.