- #1
fluidistic
Gold Member
- 3,923
- 261
Homework Statement
Hello,
I've tried all I could and get very confused about how to approach the problem.
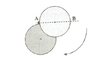
Here it comes : A disk of mass M and radius R can rotates around an axis passing by the point A without friction situated on its circumference. The disk is in a vertical plane. We let it move freely when point B is at the same high than point A and point B is opposed to point A. (See figure to get clarification).
a)What is the tangential acceleration of point B just after the disk has been released?
b)What is its velocity when it pass by its lower point?
c)What is the acceleration of point B in function of the disk's position.
2. The attempt at a solution
First I drew the applied forces, which I think are the normal and the weight. The weight is applied in the center of mass of the disk that is in its center while the normal force is applied at point A and is constantly changing so I don't even know its magnitude nor its direction.
I believe that from a formula, [tex]\vec v_{B}=\vec{\alpha}\wedge \vec{r_{B}}+\vec{a}_{CM}[/tex].
I consider the origin of the system as being the point A. I want to know [tex]\vec{a}_{CM}[/tex].
From Newton, [tex]\frac{d\vec{P}}{dt}=m\vec{a}_{CM}=\vec{F}_e=Mgj+\vec{N}\Leftrightarrow \vec{a}_{CM}=gj+\frac{\vec N}{M}[/tex].
Thanks to the right hand rule, I got that [tex]\vec{\alpha}=-\alpha k[/tex].
So [tex]\vec v_{B}=-\alpha k \wedge Ri+gj+\frac{\vec N }{M}[/tex]. The only unknowns remaining are the normal force and the angular acceleration. I've no clue how to find them.
I also tried other things, like writing down [tex]\frac{d\vec L}{dt}[/tex] or even [tex]\vec L= \vec L_o + \vec L_s[/tex] where [tex]\vec L_o[/tex] is [tex]L[/tex] orbital and [tex]\vec L_s[/tex] is [tex]L[/tex] spin. I calculated [tex]L_s[/tex] to be worth [tex]\frac{3MR^2\vec{\omega}}{4}[/tex] and I believe that [tex]L_o=\vec R_{CM} \wedge mv_{CM}[/tex] and I have much more unknowns including [tex]mv_{CM}[/tex] which seems at least as hard as to find [tex]v_{B}[/tex]...
I must be missing many things. Can you help me please?