- #1
Frank-95
- 52
- 1
Hello! It's a pretty long time time since I did my last circuit analisys, so I feel a bit rusty.
I have to calculate the evolution of current in the inductor:
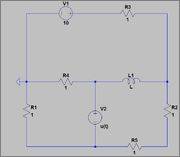
L is generic and u(t) is the Heaviside step function. Do note that at t = 0 the inductor behaves like a short circuit (I don't know the exact english term for a "full" capacitor/inductor).
Firstly I calculate the current in the inductor at iL(0-).
Hence the circuit becomes:
I found out that iL(0-) = iL(0+) = 6,6667A
At t = 0+, the second source starts to supply voltage. So I have to analise the circuit to find iL(+∞)
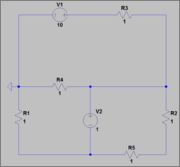
Now I am stuck because I got to some results which are different from the ones LTSpice returns.
Using the KVL clockwise I get the system:
-10 + i1 - (i1 - i2) = 0 (above mesh)
-i2 + (i1 - i2) + 1 = 0 (left below mesh)
-1 + 2i3 = 0 (right below mesh)
Which solved, gives:
i3 = 0.5 A
i2 = 10 A
i1 = 19 A
But according to LT Spice:
i3 = 0.5 A
i2 ≈ -2.66 A
i1 ≈ -6.66 A
So I don't get where I mistakened :/Second thing. After getting the right iL(+∞) I still have to get the equivalent resistence to calculate τ = L/R
Would it be a good idea to find the thevenin equivalent circuit between a and b?
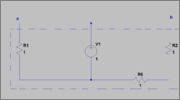
Thank you very much :)
I have to calculate the evolution of current in the inductor:
L is generic and u(t) is the Heaviside step function. Do note that at t = 0 the inductor behaves like a short circuit (I don't know the exact english term for a "full" capacitor/inductor).
Firstly I calculate the current in the inductor at iL(0-).
Hence the circuit becomes:
I found out that iL(0-) = iL(0+) = 6,6667A
At t = 0+, the second source starts to supply voltage. So I have to analise the circuit to find iL(+∞)
Now I am stuck because I got to some results which are different from the ones LTSpice returns.
Using the KVL clockwise I get the system:
-10 + i1 - (i1 - i2) = 0 (above mesh)
-i2 + (i1 - i2) + 1 = 0 (left below mesh)
-1 + 2i3 = 0 (right below mesh)
Which solved, gives:
i3 = 0.5 A
i2 = 10 A
i1 = 19 A
But according to LT Spice:
i3 = 0.5 A
i2 ≈ -2.66 A
i1 ≈ -6.66 A
So I don't get where I mistakened :/Second thing. After getting the right iL(+∞) I still have to get the equivalent resistence to calculate τ = L/R
Would it be a good idea to find the thevenin equivalent circuit between a and b?
Thank you very much :)