RLC circuit driven by a 'Real' toroid

[blargh4fun]

I'm currently wanting to model an RLC circuit that is driven by a toroid transformer with a driving current, I(t). See image below.

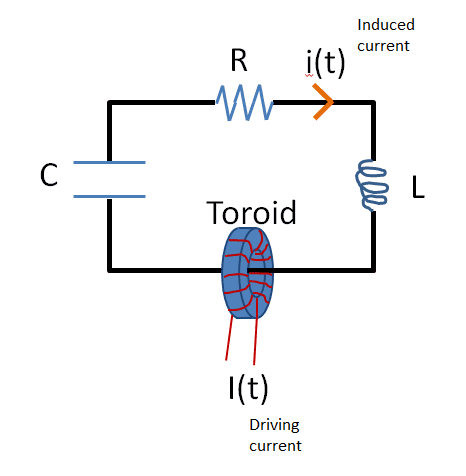
In physics class, I've done similar problems with 'ideal' toroids and a simple R circuit. What I'm struggling with is how to model a 'real' toroid transformer.

Normally I would do something like this:
$\mu_0 I_{enclosed} = \oint B \cdot dl$
$\Rightarrow B(t) = \frac{mu_0 I(t) N}{2 \pi r}$
where N is the number of turns.

The flux is equal to:
$\Phi = \int B \cdot da = \frac{mu_0 I(t) N}{2 \pi}\int \int dr dx= \frac{mu_0 I(t) N L}{2 \pi} ln\left(\frac{r_{out}}{r_{in}}\right )$
where L is the width of the toroid, and r is the inner and outer radius.

The EMF is:
$\varepsilon = -\frac{d\Phi}{dt} = - \frac{mu_0 N L}{2 \pi} ln\left(\frac{r_{out}}{r_{in}}\right ) \frac{dI(t)}{dt}$

Using Kirchoff's voltage law:
$\varepsilon = V_R + V_L + V_C = iR +\frac{di(t)}{dt}L + \frac{1}{C}\int_{-\inf}^{t}i(t)dt$

Differentiating and diving by L gives the ODE:
$\frac{d^2 i(t)}{d x^2}+\frac{R}{L}\frac{di(t)}{dt}+\frac{i(t)}{LC} = \frac{d \varepsilon (t)}{dt} \frac{1}{L}$

Which can then be solved for i(t), the induced current in the RLC circuit. Etc. Etc.

My Question Is:
Is this method ok for a 'real' toroid? I feel this is wrong because I need to include the permeability of the toroid, but I don't know how to do this. It was my understanding that the presence of a 'real' toroid strengthened the magnetic field (magnitude of 1000 or so) and subsequently increased the induced current. I will appreciate any feedback. Thanks!

 

[eljose79]

Hello! Your approach seems to be on the right track, but there are a few things to consider when modeling a 'real' toroid transformer. First, you are correct in thinking that the permeability of the toroid will affect the strength of the magnetic field and therefore the induced current. The permeability of a material is a measure of how easily it can be magnetized, and it varies depending on the material used for the toroid. So, you will need to take into account the permeability of the toroid material in your calculations. This can be done by replacing the value of \mu_0 in your equations with the permeability of the toroid material.

Additionally, the resistance of the toroid itself will also affect the circuit. This can be taken into account by including the resistance of the toroid in your Kirchoff's voltage law equation.

Lastly, it is important to consider the winding resistance of the toroid transformer. This is the resistance of the wire used to wind the transformer and can be significant in 'real' toroids. This resistance can also be included in your Kirchoff's voltage law equation.

Overall, your approach is a good starting point, but it will need to be modified to account for the permeability, resistance, and winding resistance of the toroid. I hope this helps and good luck with your modeling!