- #1
aurao2003
- 126
- 0
Homework Statement
Hi
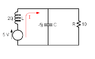
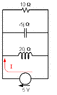
Can a kind person please check my solution? This is the question: Demonstrate the total current in an RLC parallel circuit using the following circuit. I can't draw it but the inductive reactance is 20ohms, capacitive reactance is 5ohms and resistor of 10ohms. All are in parallel. The voltage is 5v in series with 20ohms inductive reactance.
Homework Equations
The Attempt at a Solution
This is my attempted solution:
Resistive Branch: I = E/R = 5/10 = 0.5A
Capacitive Branch : E/Xc = 5/5 = 1A
Inductive Branch = E/XL =5/20 = 0.25A
Resultant current, Ix = 1 - 0.25 = 0.75A
Total current = (I^2R + I^2X)^1/2
= (0.75^2 + 0.5^2)^1/2