- #1
gfd43tg
Gold Member
- 950
- 50
Hello, I am working on this problem
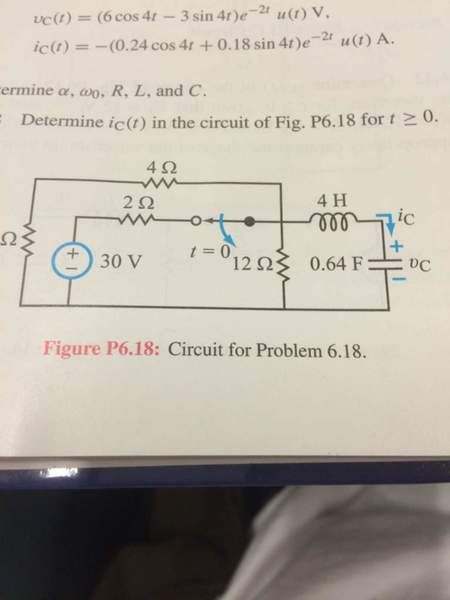
I am having some difficulty finding the right answer. A few points I'd like to expand on so that one can understand my thought process. First off, there is a standard table with the solution to series RLC circuits. I don't think I can use that table with what I have in this circuit. So one idea I have us to modify the circuit to look like what I want with a thevenin equivalent.
If the thevenin idea is wrong, I did nodal analysis and this is what my attempt looks like.

I get an expression but the initial current is Zero, which proves troubling to integrate. I also can't tell the nature of damping in this circuit either
I am having some difficulty finding the right answer. A few points I'd like to expand on so that one can understand my thought process. First off, there is a standard table with the solution to series RLC circuits. I don't think I can use that table with what I have in this circuit. So one idea I have us to modify the circuit to look like what I want with a thevenin equivalent.
If the thevenin idea is wrong, I did nodal analysis and this is what my attempt looks like.
I get an expression but the initial current is Zero, which proves troubling to integrate. I also can't tell the nature of damping in this circuit either