- #1
stunner5000pt
- 1,461
- 2
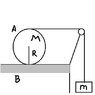
A thin string has been wound around a homogenous circular disc A in such a way that the disc can oroll on a horiz0ontal surface. The mass of the disc is M and its radius is R. The string goes around a small frictionless pulley C at a height 2Rabove the horizontal table B. To the free end of teh string is a bob of Mass M. The disc the pulley and the bob and the string are in the same vertical place.
The system begins to move under influence of gravity. The string is taut throughout and the mass of the string and pulley are negligible.
Also coefficient of friction mu is so large thte disc rolls without slipping.
Both are of same mass M so case of M doesn't matter
1. Determine the magnitude of the froce S which the string acts on the disc as long as teh systme moves under influence of gravity.
well the angle between the string and the disc is 90 so we don't haev to worry about the angle !
since there is no slipping [tex] a = \alpha R [/tex]
the components of Newton' second law
for the block mass : [tex] Ma = Mg - S [/tex]
for the disc: [tex] Ma = F [/tex] let F be the force of friction
angular components of Newton's second law
for the disc [tex] I \alpha = R (S - F) [/tex]
[tex] I \frac{a}{R^2} = S - F [/tex]
before i do any more simplification, i'd like to know if i have one everything right here ! Please do help!
2. Determine the smallest value of mu that permits the disc to roll without slipping.
firs of all when something liek a disc is involved, there is only a point that is touching the surface. But do the same rules (like those of a block) apply here too?/
so then the force of friction would be [tex] F = \mu Mg [/tex]
also [tex] Ma = F [/tex] soo, [tex] \mu Mg = Ma [/tex]
[tex] \mu = \frac{a}{g} [/tex]
is this the right direction??
The system begins to move under influence of gravity. The string is taut throughout and the mass of the string and pulley are negligible.
Also coefficient of friction mu is so large thte disc rolls without slipping.
Both are of same mass M so case of M doesn't matter
1. Determine the magnitude of the froce S which the string acts on the disc as long as teh systme moves under influence of gravity.
well the angle between the string and the disc is 90 so we don't haev to worry about the angle !
since there is no slipping [tex] a = \alpha R [/tex]
the components of Newton' second law
for the block mass : [tex] Ma = Mg - S [/tex]
for the disc: [tex] Ma = F [/tex] let F be the force of friction
angular components of Newton's second law
for the disc [tex] I \alpha = R (S - F) [/tex]
[tex] I \frac{a}{R^2} = S - F [/tex]
before i do any more simplification, i'd like to know if i have one everything right here ! Please do help!
2. Determine the smallest value of mu that permits the disc to roll without slipping.
firs of all when something liek a disc is involved, there is only a point that is touching the surface. But do the same rules (like those of a block) apply here too?/
so then the force of friction would be [tex] F = \mu Mg [/tex]
also [tex] Ma = F [/tex] soo, [tex] \mu Mg = Ma [/tex]
[tex] \mu = \frac{a}{g} [/tex]
is this the right direction??