Is My Approach to Calculating the Length of a Rotating Compound Pulley Correct?

[wirefree]

I am appreciative of the opportunity afforded by this forum to submit a query.

Problem: See

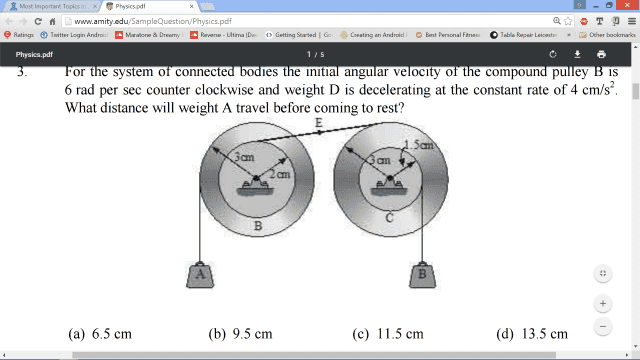
NOTE: The reference to weight "D" in the second line is incorrect.

My Attempt:
Step 1: Since this is a constant acceleration situation, I calculated the angular acceleration = 3 cm * -4 cm/s/s
Step 2: Employed the constant acceleration equation $$\omega^2 = \omega_0^2 + 2*\alpha*\theta$$ to obtain $$\theta = 3/2$$
Step 3: Lastly, I converted angle to length for the disc of radius 3 cm to obtain the required answer as 14.13 cm.Question: This approach does not yield. What should I relook?

Look forward to your suggestion.wirefree

 

[andrewkirk]

Step 1: Since this is a constant acceleration situation, I calculated the angular acceleration = 3 cm * -4 cm/s/s

There are two errors in this calculation:

1. To get the angular acceleration, you divide the linear acceleration by the radius, not multiply it, as was done here.
2. The radius is that at which the rope from B attaches to the pulley, which is 1.5cm, not 3cm.

If you correct these two errors, you should get a correct $\theta$, which will enable you to get the correct answer.

 

[wirefree]

Many thanks for the correction, Andrew (Capt) Kirk. I apologize for having submitted the solution with such carelessness. I suspect that the carelessness really is simply a reflection of a lack of faith in the approach I adopted.

Unfortunately, the reworking has only corroborated my suspicion. Here is the reworked solution which, too, doesn't yield:

Step 1: $$\alpha = \frac{-4}{1.5} = \frac{-8}{3}$$
Step 2: $$0 = 6^2 + 2*\frac{-8}{3}*\theta$$ Therefore, $$\theta = \frac{27}{4}$$
Step 3: $$2*\pi$$ radians = Circumference of 3 cm pulley = $$2*\pi*3$$ cm. Therefore, $$\frac{27}{4}$$ radians equals $$20.25 cm$$

Look forward to your advice.wirefree

 

[andrewkirk]

You have the angle traveled by the right-hand pulley as 27/4 radians.
The next step is to work out the angle traveled by the left-hand pulley, based on the gearing applied by the ratio of the two radii at which the pulleys are connected by a rope.

 

[Merlin3189]

You seem to be getting there.
When you have finished, you might like to try the opposite approach, of working with linear motion of A and B (or D as it should be labelled.)

For A, linear (circumfrential) speed = angular speed x radius = 6 rad/s x 3cm = 18 cm/sec (v=ωr may be the relation you are not familiar with?)
Gearing = 3/2 x 3/1.5 = 3
So linear speed of B (D) = 18/3 = 6 cm/s
For block B (D) v² = u² + 2as with u = 6 cm/s, a = - 4 cm/s²
Then distance for block A is geared down 3x, so = s/3

Or even simpler, just work with block A and gear up the acceleration to 3 x -4 cm/s²
So v² = u² + 2as with u = 18 cm/s, a = - 12 cm/s²
The only snag with that is it's harder to do all the sums in your head, unless you know 18²

 

[andrewkirk]

I've just realized that the problem has two different things called B. One is the left-hand pulley and the other is the right-hand weight. Add that to the fact that they then refer to a D that is not even in the diagram, and no wonder the whole thing makes no sense. Different answers will be available depending on whether the reference to D was supposed to be to A or to B. It needs to be B to make the problem come out, but it could have been either.

The calcs we were doing assumed that the angular speed of 6 rad/s applied to the RH pulley - because that has weight B on it - and they don't come out with one of the answers. But if we do them with the 6 rad/s being the ang veloc of the LH pulley as Merlin did then the problem works out.

So don't feel bad that you find the problem difficult @wirefree. The fault lies with whoever wrote the problem.

 

[Merlin3189]

Quite agree with you about the question. I had to wonder where D should be. Four things decided it for me:
B has to be a pulley because it is rotating at 6 rad/sec and it is irrelevant whether the mass labelled B is rotating or not.
the LH pulley is labelled B
A and D are called weights
if the right hand mass were D then the letters would go left to right, ABCD
When the calculations worked so nicely and gave one of the answers, that sealed it!

At first I thought I wouldn't be bale to solve it without knowing the moments of inertia of the pulleys and the mass of the weights, but they all seem to be subsumed in the constant acceleration. That's why I didn't see the need to look at anything other than the linear motion of the masses.

 

[wirefree]

Having been advised to abandon the initial approach, I am inclined to pause and, instead, learn from you two gentlemen the key idea. To make this convenient for you, I request you to respond to the following one question:

Why doesn't the angular acceleration of the L.H. pulley equal that of the R.H. pulley?

Look forward to your response.wirefree

 

[Merlin3189]

String E is the key. It wraps around both pulleys.
If this E string moves 6cm, the pulley B must rotate 3x, but pulley C only rotates 2x.
So if B is rotating at 6 rad/sec, C only needs to rotate at 4 rad/sec, (and the string E moves at 12 cm/sec.)

The ratio between the angular speeds is determined by ratio of radii = 2 : 3
So ω_C : ω_B = 2 : 3

Just as their speeds are tied together by string E, so are their accelerations. You can look at this in several ways.
One way: B rotates at 6 rad/s, so C rotates at 4 rad/sec. They both stop at the same time (in fact after 1.5 sec.)
So accn B = -6 rad/sec / 1.5 sec = -4 rad/sec²
and accn C = -4 rad/sec /1.5 sec = -2.67 rad/sec²

These are also connected by the ratio of radii, accn C : accn B = 2 : 3
So you could say, if accn B is -4 rad/sec², then accn C = -4rad/sec x 2/3 = -2.67 rad/sec.

BTW I'm not saying you should give up on your approach. You had me confused at first, but now I see your method of considering angular speed and acceleration is exactly parallel to the linear equations. I converted the angular speed to linear speed, then did linear motion: you converted linear acceleration to angular acceleration, then used angular motion.

 

[andrewkirk]

@wirefree your approach was fine.

The only problem was that, like me, you assumed that the initial angular velocity of 6 rad/s applied to the right-hand pulley rather than the left-hand one. We were fooled by the right-hand weight being labelled B and the label B on the left-hand pulley being less prominently displayed, so that I didn't notice it until Merlin pointed it out. So the only change you need to make to your approach is to convert the 6 rad/s initial angular velocity of the LH pulley to an initial angular velocity of the RH pulley, which means multiplying 6 by the gearing ratio 2/3, to get 4 rad/s as the initial ang veloc of the RH pulley. If you put that into your equations below instead of 6, you should be on the track to a correct answer.

Here is the reworked solution which, too, doesn't yield:

Step 1: $$\alpha = \frac{-4}{1.5} = \frac{-8}{3}$$
Step 2: $$0 = 6^2 + 2*\frac{-8}{3}*\theta$$ Therefore, $$\theta = \frac{27}{4}$$
Step 3: $$2*\pi$$ radians = Circumference of 3 cm pulley = $$2*\pi*3$$ cm. Therefore, $$\frac{27}{4}$$ radians equals $$20.25 cm$$

That will give you the total angle traveled by the RH pulley. THen convert that to an angle for the LH pulley by dividing by the gearing ratio (divide by 2/3, ie multiply by 3/2), then multiply by the radius at which the LH pulley attaches, and you'll get one of the offered answers.

 

[wirefree]

@Merlin3189 Thank you, Sir.

@andrewkirk: You give me more credit than I deserve, Captain. I had attributed the angular velocity to pulley B knowingly, as I acknowledged by submitting my last query.

I stand better informed now. Thank you both of you Gentlemen for your collectively two-pronged approach to what was my problem.wirefree (aka Gaurav)