- #1
Niles
- 1,866
- 0
Homework Statement
Hi
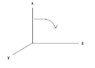
I have a coordinate system as attached, and I want to rotate it along the y-axis in the clockwise direction as shown. For this purpose I use
[tex]
R = \left( {\begin{array}{*{20}c}
{\cos \theta } & 0 & {\sin \theta } \\
0 & 1 & 0 \\
{ - \sin \theta } & 0 & {\cos \theta } \\
\end{array} } \right)
[/tex]
where θ<0 since I rotate CW. Say I now look at the point (x, y, z) = (1, 0, 1). This I want to rotate by θ=-45 degrees, which then becomes in the new system (x', y', z') = (0, 0, 1/√2). But that is wrong, according to my figure (which satisfies the right-hand rule) it should give (x', y', z') = (1/√2, 0, 0).
I thought I had followed the convention with the right-hand rule, but I must have made an error somewhere. I can't figure out where it is though, it seems consistent. I would be happy to get some feedback.Niles.
Attachments
Last edited: