Rotational energy variables

[MathewsMD]

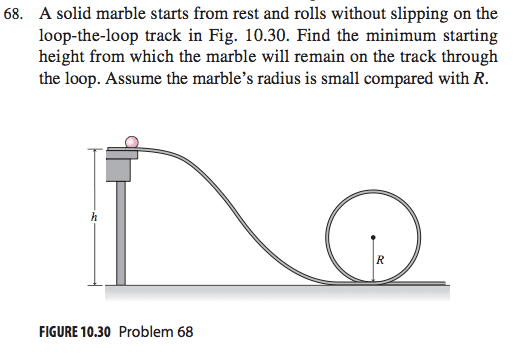
A solid marble starts from rest and rolls without slipping on the loop-the-loop track in Fig. 10.30. Find the minimum starting height from which the marble will remain on the track through the loop. Assume the marble’s radius is small compared with R.

Solution:

In the question, why is the radius of the circle referred to as R-r instead of just R? Is this common notation since I'm having a little bit of trouble understanding what exactly r is in this case and how this form helps us assess the situation. Also, why must v >= g (R-r)? I think this question stems from my previous one, but if the forces at the top must be at least F_n + mg, why isn't v >= (gr)^0.5 since then v²/r >= g at the top for there to be a normal force still, correct?

Any help would be great! :)

 

[MuIotaTau]

$r$ is the radius of the ball, so the distance from the center of the loop-de-loop to the center of mass of the ball is just the full radius of the loop, $R$, minus the distance the center of mass of the ball is raised up from the edge of the loop, $r$. Make sense? And so the equation they arrive at for the minimum velocity, $v^2 \geq \sqrt{g(R - r)}$, matches what you have, provided that you use $R - r$.

 

[MathewsMD]

$r$ is the radius of the ball, so the distance from the center of the loop-de-loop to the center of mass of the ball is just the full radius of the loop, $R$, minus the distance the center of mass of the ball is raised up from the edge of the loop, $r$. Make sense? And so the equation they arrive at for the minimum velocity, $v^2 \geq \sqrt{g(R - r)}$, matches what you have, provided that you use $R - r$.

Haha okay, wow that does make sense. They stated in the question r is small compared to R so I thought we did not consider it. Thanks for the clarification!

 

[MuIotaTau]

Yeah, sure thing! Actually, given that they said the radius of the ball is small, I would actually be very confused too if I hadn't been working backwards from the solution, so I don't blame you at all.

 

[Nickie]

Hi there,

Thank you for your questions regarding rotational energy variables and the loop-the-loop track scenario. Let's break down the different components of this problem and address your questions one by one.

First, let's define the variables in this scenario. The solid marble has a certain radius, which we will call r, and it starts from rest at a certain height, which we will call h. The track itself has a larger radius, which we will call R. The question specifies that r is small compared to R, meaning that r << R.

Now, let's address your first question about the notation R-r. This is simply a way to represent the distance between the center of the marble and the top of the track, as shown in the figure. Since the track has a larger radius, we can think of R as the total distance from the center of the track to the top, and r as the distance from the center of the track to the center of the marble. Therefore, R-r represents the remaining distance from the center of the marble to the top of the track.

Moving on to your second question about the condition v >= g (R-r). This is known as the rolling without slipping condition, which means that the speed of the marble must be greater than or equal to the speed it would have if it were simply sliding down the track without rolling. This condition ensures that the marble maintains contact with the track at all times and does not slip off. The value of v is determined by the conservation of energy principle, where the initial potential energy of the marble at height h is converted into kinetic energy as it rolls down the track. The term g (R-r) represents the change in potential energy and must be greater than or equal to the kinetic energy for the marble to remain on the track.

Finally, your last question about the normal force at the top of the track. You are correct in saying that the normal force at the top must be equal to the sum of the gravitational force and the centripetal force (Fn + mg). However, the condition v >= g (R-r) ensures that the marble has enough speed to maintain this normal force, as the centripetal force is dependent on the speed of the marble.

I hope this helps clarify the concepts and reasoning behind the solution to this problem. Keep in mind that rotational energy and motion can be quite complex, so it's important to carefully consider all the different variables and conditions in a scenario like this