- #1
Maximusflash
Hey guys
I do apologize in advance for any errors or misunderstandings in my question, been that english is not my native language.
I was wondering how to calculate the RPM of a gear (or a wheel) applied with a known force. I'm guessing I'm not using the correct terminologies using Google, because I seem to not find exactly what I'm looking for.
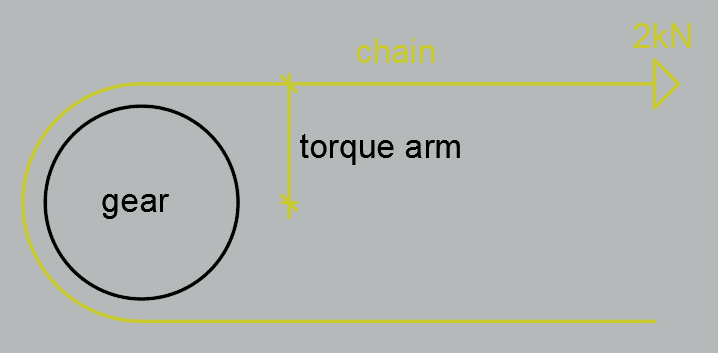
Let's say you have some sort of pulley system or a bike gear for that matter. If one where to apply a constant force of f.ex 2kN to this pulley: what RPM will the gear have? It will of course be relative to the radius of the gear, which again will be important for the torque. So for the sake of calculating with numbers, let's say the gear is 1m across, making the radius 0.5m. So toques is 2kN x 0.5m = 1kNm.
But I can't seem to figure out how to calculate the RPM of the gear.
Anyone who can push me in the right direction?
I do apologize in advance for any errors or misunderstandings in my question, been that english is not my native language.
I was wondering how to calculate the RPM of a gear (or a wheel) applied with a known force. I'm guessing I'm not using the correct terminologies using Google, because I seem to not find exactly what I'm looking for.
Let's say you have some sort of pulley system or a bike gear for that matter. If one where to apply a constant force of f.ex 2kN to this pulley: what RPM will the gear have? It will of course be relative to the radius of the gear, which again will be important for the torque. So for the sake of calculating with numbers, let's say the gear is 1m across, making the radius 0.5m. So toques is 2kN x 0.5m = 1kNm.
But I can't seem to figure out how to calculate the RPM of the gear.
Anyone who can push me in the right direction?