- #1
karush
Gold Member
MHB
- 3,269
- 5
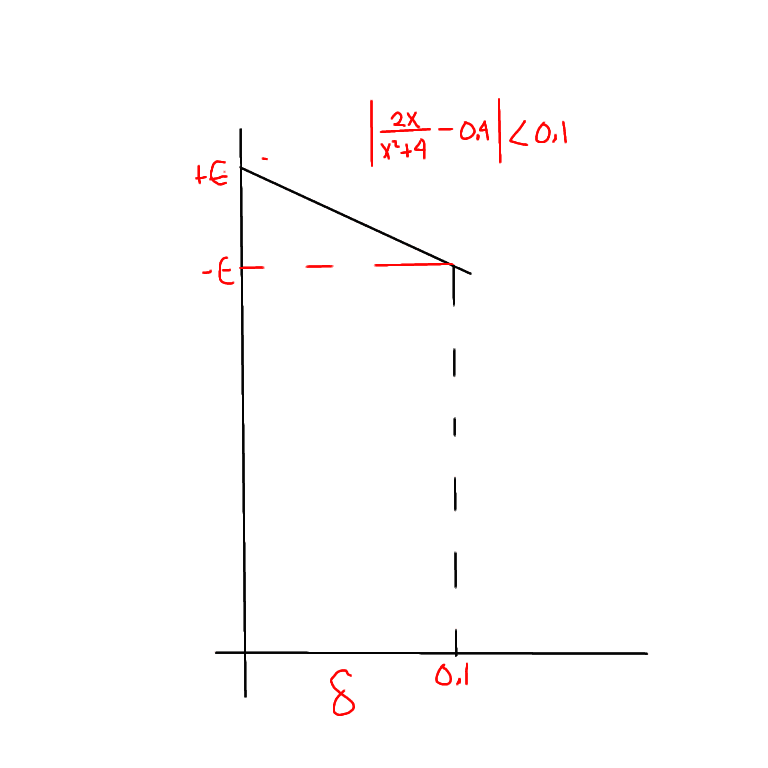
Find a graph to a number $\delta$ such that
$$\textit{if }
|x-1|<\delta
\textit{ then }
\left|\dfrac{2x}{x^2+4}-0.4\right|<0.1
$$
ok I always had a very hard time doing these I did look at some examples but still ?
did a ibispaint drawing to start basically it looks like we are finding the dimenstions of box given the parameters
$$\textit{if }
|x-1|<\delta
\textit{ then }
\left|\dfrac{2x}{x^2+4}-0.4\right|<0.1
$$
ok I always had a very hard time doing these I did look at some examples but still ?
did a ibispaint drawing to start basically it looks like we are finding the dimenstions of box given the parameters