Sailboat Race Vectors Paroblem

[vane12]

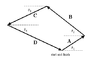
A sailboat race course consists of four legs defined by the displacement vectors A, B, C and Dshown above.
The values of the angles are Θ1 = 35.00, Θ2 = 34.00, andΘ3 = 20.00.
The magnitudes of the first three vectors are A = 3.0 km, B = 5.0 km and C = 4.5 km. The finish line of the course coincides with the starting line.
The coordinate system for this problem has positive x to the right, positive y as up and counter-clockwise to be a positive angle.
1) What is the distance of the fourth leg?
2) What is the value of Θ4?
3) What is the value of Dy?

To solve the problem I did the following:

Ax = 3cos35°
Ay = 3sin35°
Bx = 5cos146°
By = 5sin146°
Cx = 4.5cos 20°
Cy = 4.5sin20°

Somehow I was able to get the right answer of the fourth leg but not for Dy or the angle.

 

[rl.bhat]

From the given data, you can find the angle between A and B. From that you can find the resultant R of A and B using cosine rule. Next using sine rule, you can find the angle between A and R and B and R. That gives you the angle between R and C. Similarly proceed to find the fourth leg and θ₄.