How can the energy of an orbit determine the size of its semimajor axis?

[Tanya Sharma]

Homework Statement

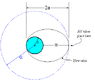
A satellite is moving in a circular orbit around a massive planet of radius R. The altitude of the satellite above the surface of the planet is 3R and its speed is v. In order to place the satellite in an elliptical orbit which will bring it closer to the planet ,its velocity is reduced from v to μv., where μ<1 . The smallest permissible value of μ if the satellite is not to crash on the surface of planet is √(2/K), find K .

Homework Equations

The Attempt at a Solution

Orbital speed of the satellite $v = \sqrt{\frac{GM}{4R}}$

KE of the satellite = $\frac{GMm}{8R}$

PE of the satellite = $-\frac{GMm}{4R}$

$E = -\frac{GMm}{8R}$

Just after the speed is reduced , KE₁ = $\frac{1}{2}mμ^2v^2 = \frac{μ^2GMm}{8R}$

PE₁ = $-\frac{GMm}{4R}$

$E_1 = \frac{μ^2GMm}{8R} -\frac{GMm}{4R}$

$E_1 = \frac{GMm}{4R}(\frac{μ^2}{2}-1)$

The semi major axis 'a' of the new orbit will be given by $\frac{1}{a} = \frac{1}{2R}(1-\frac{μ^2}{2})$

Or, $a = \frac{4R}{2 - μ^2}$

The planet would be at one of the focii of the orbit.

The minimum distance of the satellite from the planet will be a(1-e) where ‘e’ is the eccentricity of the elliptical orbit .

If the satellite is not to crash then a(1-e) > 0 or a>0 . Is this the condition we need to use ?

I am not sure if I have approached the problem correctly .

I would be grateful If someone could help me with the problem.

 

[gneill]

You can assume that the mass of the satellite is negligible with respect to that of the planet.

Hint: Investigate the specific energy of the new orbit assuming a gravitational parameter $\mu_p$ for the planet. How is it related to the semimajor axis of the orbit?

 

[ehild]

The minimum distance of the satellite from the planet will be a(1-e) where ‘e’ is the eccentricity of the elliptical orbit .

If the satellite is not to crash then a(1-e) > 0 or a>0 . Is this the condition we need to use ?

The orbit parameters (closest and farthest points) are measured from the focus of the ellipse and the focus is in the centre of the massive planet (the mass of the satellite is negligible).

How far is the satellite from the centre of the massive planet when it crashes with it? ehild

 

[Tanya Sharma]

How far is the satellite from the centre of the massive planet when it crashes with it?

The satellite would be at distance R .

So should I use a(1-e) > R ? If yes , then we don't know the value of 'e' .

 

[Tanya Sharma]

You can assume that the mass of the satellite is negligible with respect to that of the planet.

Hint: Investigate the specific energy of the new orbit assuming a gravitational parameter $\mu_p$ for the planet. How is it related to the semimajor axis of the orbit?

Sorry...what is specific energy and what is $\mu_p$ ? I haven't used these terms before .

 

[ehild]

You do not need to use anything else but conservation of angular momentum and energy (and that the centripetal force is equal to the force of gravity) ehild

 

[Tanya Sharma]

Is the point at which the speed is reduced either of the two (perihelion or aphelion) ? Or is it any other point on the elliptical orbit ? How do we know ?

 

[gneill]

Sorry...what is specific energy and what is $\mu_p$ ? I haven't used these terms before .

The gravitational parameter $\mu_p$ is just shorthand for GM for the planet.

Specific mechanical energy for an orbiting object is defined as the energy per unit mass of the object. It's the sum of the specific kinetic energy and specific potential energy (also per unit mass). It's used because in almost every case the mass of the orbiting object is negligible with respect to the primary it's orbiting, and its mass variable always cancels out of the equations eventually anyways.

So to be clear, the specific mechanical energy $\xi$ is given by:
$$\xi = \frac{v^2}{2} - \frac{\mu_p}{r}$$
Just multiply $\xi$ by m to recover the "actual" energy of the object, if m is its mass.

It also happens to be related to the size of the orbit's semimajor axis:
$$\xi = -\frac{\mu_p}{2a}$$
In your problem you can determine the semimajor axis for the "new" orbit quite easily if yuo make a sketch.

 

[Tanya Sharma]

Thanks for explaining the terms .

Isn't $a = \frac{4R}{2 - μ^2}$ ?

 

[gneill]

Is the point at which the speed is reduced either of the two (perihelion or aphelion) ? Or is it any other point on the elliptical orbit ? How do we know ?

The original orbit is circular and its speed is suddenly reduced to turn it into an elliptical orbit. This reduces the kinetic energy of the orbit at that point, yet its potential energy remains the same. So overall its mechanical energy is reduced for a smaller orbit. Since circular and elliptical orbits are closed curves, the point where the speed change took place must be in common to both the "old" and "new" orbits.

All this to say that the point where the speed is reduced becomes the aphelion (Sun orbit) or apogee (planetary orbit).

 

[gneill]

Thanks for explaining the terms .

Isn't $a = \frac{4R}{2 - μ^2}$ ?

I'm not seeing where that comes from. You can just read "a" directly from a sketch of the obits.

 

[Tanya Sharma]

gneill...Thank you very much for the sketch .I could not have visualized the situation , if you would not have made the picture .

Well...I guess I am having problem with the basics of gravitation. But you have been extremely nice .

The original orbit is circular and its speed is suddenly reduced to turn it into an elliptical orbit. This reduces the kinetic energy of the orbit at that point, yet its potential energy remains the same. So overall its mechanical energy is reduced for a smaller orbit. Since circular and elliptical orbits are closed curves, the point where the speed change took place must be in common to both the "old" and "new" orbits.

You are right . I did take this into consideration in post#1 .

But how does this explain that the satellite is at aphelion and not perihelion or any other point of the orbit?

Sorry for my lack of understanding .

 

[Tanya Sharma]

From the sketch , a =5R/2

Now β²v²/2 - GM/4R = -GM/2a

β²GM/8R - GM/4R = -GM/5R

β²GM/8 - 1/4 = -1/5

Solving , I get β = √(2/5)

Hence k=5 .

Is it correct ? I don't have the answer key .

Edit: I have used β instead of μ(as originally given in the question) so as to avoid confusion with the use of μ_P i.e gravitational parameter .

 

[gneill]

gneill...Thank you very much for the sketch .I could not have visualized the situation , if you would not have made the picture .

Well...I guess I am having problem with the basics of gravitation. But you have been extremely nice .



You are right . I did take this into consideration in post#1 .

But how does that explains that the satellite is at aphelion and not perihelion or any other point of the orbit?

Sorry for my lack of understanding .

The energy of an orbit specifies the size of its semimajor axis. Apogee and Perigee lie at either end of this axis. Since the elliptical orbit has been given a smaller energy than the original orbit, its semimajor axis is reduced in size. The semiminor axis of an ellipse is always smaller than the semimajor axis. Together this means that the elliptical orbit must lie within the bounds of the original circular orbit (its smaller and fits inside. See the image in post #11). As the orbits must touch at the point the change was made, this makes that point an extrememum of the smaller orbit. i.e. apogee.

Another way to look at it is that the new velocity of the object is insufficient to support circular motion at its then current position, so as it moves away from that location it must fall closer to the planet. By time symmetry (orbit has the same shape if time runs forwards or backwards) that make the current point the extremum which is the furthest point from the focus (apogee).

 

[gneill]

From the sketch , a =5R/2

Now β²v²/2 - GM/4R = -GM/2a

β²GM/8R - GM/4R = -GM/5R

β²GM/8 - 1/4 = -1/5

Solving , I get β = √(2/5)

Hence k=5 .

Is it correct ? I don't have the answer key .

It looks good to me

 

[Tanya Sharma]

The energy of an orbit specifies the size of its semimajor axis. Apogee and Perigee lie at either end of this axis. Since the elliptical orbit has been given a smaller energy than the original orbit, its semimajor axis is reduced in size. The semiminor axis of an ellipse is always smaller than the semimajor axis. Together this means that the elliptical orbit must lie within the bounds of the original circular orbit (its smaller and fits inside. See the image in post #11). As the orbits must touch at the point the change was made, this makes that point an extrememum of the smaller orbit. i.e. apogee.

Another way to look at it is that the new velocity of the object is insufficient to support circular motion at its then current position, so as it moves away from that location it must fall closer to the planet. By time symmetry (orbit has the same shape if time runs forwards or backwards) that make the current point the extremum which is the furthest point from the focus (apogee).

Brilliant ! Absolutely brilliant . Nowhere did I find such a nice and logical explanation.

Thank you so...much .

You are a fantastic mentor .