- #1
likephysics
- 636
- 2
π²³ ∞ ° → ~ µ ρ σ τ ω ∑ … √ ∫ ≤ ≥ ± ∃ · θ φ ψ Ω α β γ δ ∂ ∆ ∇ ε λ Λ Γ ô
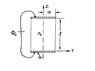
Consider the cylindrical in free space as shown below. The resistor has diameter 2a, length l, is filled with a inhomogeneous material with a z dependent electrical conductivity σ(z) and is capped by 2 thin disks of materials with infinite conductivity. A static voltage φ0 is applied to the 2 disks with a battery.
Show that the potential inside the battery is given by
φ (z)= ∫ (C1/σ(z)) dz+ C2
C1,C2 are constants
I am trying to use poisson's equation in cylindrical coordinates.
But I am not sure, how to get the right hand side
The potential varies only along Z and is constant along r and φ
Therefore, poissons eqn will reduce to
d2(φ)/dz2 = -ρ/ε
I need σ(z) on the right hand side, but I have ρ/ε. How do I arrive at σ(z)?
Homework Statement
Consider the cylindrical in free space as shown below. The resistor has diameter 2a, length l, is filled with a inhomogeneous material with a z dependent electrical conductivity σ(z) and is capped by 2 thin disks of materials with infinite conductivity. A static voltage φ0 is applied to the 2 disks with a battery.
Show that the potential inside the battery is given by
φ (z)= ∫ (C1/σ(z)) dz+ C2
C1,C2 are constants
Homework Equations
The Attempt at a Solution
I am trying to use poisson's equation in cylindrical coordinates.
But I am not sure, how to get the right hand side
The potential varies only along Z and is constant along r and φ
Therefore, poissons eqn will reduce to
d2(φ)/dz2 = -ρ/ε
I need σ(z) on the right hand side, but I have ρ/ε. How do I arrive at σ(z)?