- #1
Quentin_C
- 19
- 0
Hi all I hope you can help me with the statistical origins of the Second Law. I cannot find anything that mathematically proves that order from disorder is impossible only improbable.
Leading me to think that a system (Kelvin engine) that allows order to be created from disorder (work from ambient temp) is possible if it is probable.
To be more specific what prevents fundamentally prevents unidirectionality.
Can someone assist to shoot this down? Help me move on !
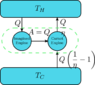
Working down from
Or framed another way
Isn’t the equivalence argument cyclical as if the imagined Kelvin Engine is generated from an original statistical bias (a way to create order from disorder) then all the assumptions proving this are baseless as we are just using a the absence of statistical bias to prove we can’t have a statistical bias ?
This is the assumption that I ask you to suspend – Assume that a fixed number of microstates all are equally probable and all microstates encourage order.
The scenario I propose (however far-fetched) is one where order can be created by movement between fixed equally probable microstates at static** temperature–
Can anyone help??
Before we bring them up the to me Smoluchowski trapdoor , Brownian Ratchet all only prove that if all microstates are equally probable then no net work can be extracted as states that extract work are equally probable as states that require work. Not that a bias can assure only positive states are probable.
Leading me to think that a system (Kelvin engine) that allows order to be created from disorder (work from ambient temp) is possible if it is probable.
To be more specific what prevents fundamentally prevents unidirectionality.
Can someone assist to shoot this down? Help me move on !
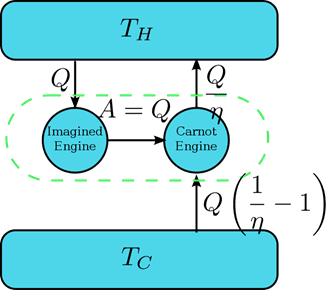
Working down from
- Entropy a statistical law which says that it is highly improbable that an equilibrium state will occupy anything but the most probable (disordered states)
Supports - Second law of thermodynamics states that the arrow of time will only ever allow disorder to evolve travel from the current (ordered) state to a more probable (disordered) state
Supports - Claussis statement heat will never travel from cool to hot (without work) as the resultant equilibrium microstate (of the system) is not the most probable therefore entropy would decrease.
Supports - Kelvin Statement – heat can never be extracted and made to do work from a single reservoir heat source as this is allows and is equivalent to/and would allow the Claussis statement.
Or framed another way
Isn’t the equivalence argument cyclical as if the imagined Kelvin Engine is generated from an original statistical bias (a way to create order from disorder) then all the assumptions proving this are baseless as we are just using a the absence of statistical bias to prove we can’t have a statistical bias ?
This is the assumption that I ask you to suspend – Assume that a fixed number of microstates all are equally probable and all microstates encourage order.
The scenario I propose (however far-fetched) is one where order can be created by movement between fixed equally probable microstates at static** temperature–
- Fixed Microstates - Entropy does not increase nor decrease.
- Equally Probable – the equilibrium microstate is the most probable.
- Static Temp - as work (order) is extracted that TH constantly resupplies TC so they can be assumed fixed and are so identical over time
Can anyone help??
Before we bring them up the to me Smoluchowski trapdoor , Brownian Ratchet all only prove that if all microstates are equally probable then no net work can be extracted as states that extract work are equally probable as states that require work. Not that a bias can assure only positive states are probable.
Attachments
Last edited: