Self Energy for N flavor phi^4 theory

[psi*psi]

I am reading the fifth chapter on perturbation theory of Condensed Matter Field Theory by Altland and Simons. This question is about the section starting on page 223.

To discuss self energy, they introduced a vector field $\phi = \{ \phi^a \}, a = 1, \cdots , N$. The action of the field is given by
$$S[\phi] = \int d^dx (\frac{1}{2} \partial \phi \cdot \partial \phi + \frac{r}{2} \phi \cdot \phi + \frac{g}{4 N} (\phi \cdot \phi)^2)$$
The goal is to compute the perturbation expansion of the Green function
$$G^{ab}(x-y)=\langle \phi^a (x) \phi^b (y)\rangle$$
using the self energy operator $\Sigma_p$.

In momentum space, the Green function is given by
$$G^{ab}_{p} = [(p^2+r- \hat \Sigma_p)^{-1}]^{ab},$$
where the diagrams for $\Sigma_p$ is shown in the figure

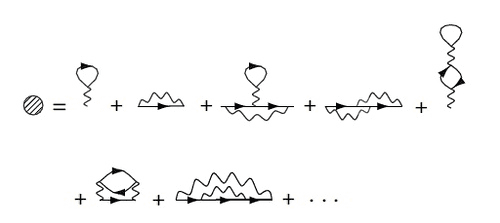
The text claims that represented in terms of the Green functions, the first order contribution to the self-energy operator is given by
$$[\Sigma^{(1)}_{\mathbf{p}}]^{ab} = - \delta^{ab} \frac{g}{L^d} (\frac{1}{N} \sum_{\mathbf{p'}} G_{0,\mathbf{p'}} + \sum_{\mathbf{p'}} G_{0,\mathbf{p-p'}}),$$
where the first (second) term in the parenthesis corresponds to the first (second) diagram in the figure. I am having trouble reproducing this result. Specifically,
(1) Where does the overall minus sign come from?
(2) Since the interaction strength is given by $g/4N$, from the result, the first diagram has a contribution of $4$ and the second diagram has a contribution of $4N$. How do I get these factors?
(3) How do I derive the Feynman rules for these diagrams?

Thanks.

 

[eljose79]

Hello,

Thank you for sharing your question about perturbation theory and self energy in condensed matter field theory. I am happy to help clarify some of the points you mentioned.

Firstly, the overall minus sign in the expression for the first order contribution to the self-energy operator comes from the minus sign in the interaction term in the action. This is a standard convention in quantum field theory, where the interaction term is considered to be a "source" for the field and therefore has a negative sign.

Secondly, the factor of 4 in the contribution from the first diagram comes from the fact that there are 4 different ways to contract the two fields in the diagram. This is known as the "symmetry factor" and is a common feature in Feynman diagrams. For the second diagram, the factor of 4N comes from the fact that there are N different ways to contract the two fields in the diagram, and each of these ways has a factor of 4 from the previous explanation.

Lastly, to derive the Feynman rules for these diagrams, you can use the standard rules for Feynman diagrams, which include propagators (lines) representing the Green function, vertices representing interactions, and momentum conservation at each vertex. The self-energy operator can be thought of as a correction to the propagator, so in this case, we have a propagator with a "hat" on top representing the self energy correction. For more detailed explanations and examples of Feynman rules, I recommend consulting a textbook or online resources on perturbation theory in quantum field theory.

I hope this helps clarify some of your questions. Best of luck with your studies!