- #1
fluppocinonys
- 19
- 1
1.
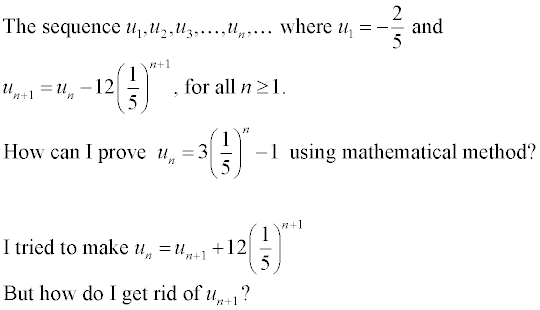
2.
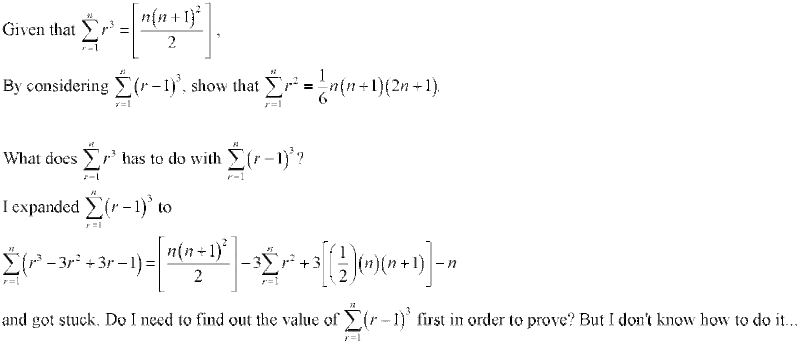
3.
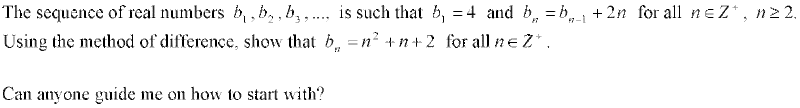
2.
3.
Last edited:
CompuChip said:Can you write down that "proof" a bit more clearly? Because I have no idea what it is you were doing there.
For the first one, I suggested a proof by induction. Have you seen that technique before?
Sequences and series problems are mathematical problems that involve finding a pattern or formula for a sequence or series of numbers. A sequence is a list of numbers that follow a specific pattern, while a series is the sum of a sequence of numbers.
The next term in a sequence can be found by identifying the pattern and applying it to the next term. This can involve adding or subtracting a constant number, multiplying or dividing by a constant number, or using a more complex formula.
An arithmetic sequence is a sequence in which each term is obtained by adding a constant number to the previous term. A geometric sequence is a sequence in which each term is obtained by multiplying the previous term by a constant number. In an arithmetic sequence, the difference between consecutive terms is constant, while in a geometric sequence, the ratio between consecutive terms is constant.
The sum of a finite arithmetic series can be found by using the formula Sn = (n/2)(a1 + an), where Sn is the sum, n is the number of terms, and a1 and an are the first and last terms of the series. The sum of a finite geometric series can be found by using the formula Sn = a1((1-r^n)/(1-r)), where Sn is the sum, a1 is the first term, r is the common ratio, and n is the number of terms.
Sequences and series problems can be applied in various fields such as finance, physics, and computer science. For example, in finance, the compound interest formula is a geometric series formula used to calculate the future value of an investment. In physics, the equations of motion for uniformly accelerated motion can be represented as arithmetic sequences. In computer science, algorithms use sequences and series to efficiently perform calculations and solve problems.