- #1
neiks997
- 3
- 0
Homework Statement
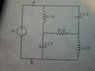
I will give a circuit of 5 passive components and an AC voltage source producing a sinusoidal voltage at a fixed frequency of omega / (2*pi) Hz.
i will post a picture asking what is being looked for along with the circuit.
Homework Equations
z = R + jwL + 1 / jwc, jw0L + 1 / jw0c = 0, w0 = 1/ sqrt(LC), B = w2 - w1 = R/L = w0/Q, Q = w0L / R = 1/w0RC, w1 = w0 - B/2, w2 = w0 + B/2
The Attempt at a Solution
clueless on how to make an equivalent circuit.