- #1
juicev80
- 1
- 0
Homework Statement
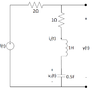
I attached a picture of the circuit.
f(t) = (e-t)u(t), VC(0-) = 2V, iL(0-) = 1A
Obtain an expression for the total response, y(t), for the given system by finding
the natural and the forced responses.
Homework Equations
v(t) = Ri(t)
v(t) = Ldi(t)/dt
v(t) = (1/C)∫i(t)dt
The Attempt at a Solution
Ok, the first thing I did was combine the two series resistors. What I am thinking is that I will solve for the response of i(t) and then sub that into the formula f(t) - R2Ω*i(t) = y(t). I feel like there should be a way to solve for the voltage y(t) directly, but I haven't been able to figure out how to setup the equation.
So, solving for the response of i(t) I do KVL and get 3i(t) + di(t)/dt + 2[itex]\int[/itex]i(t)dt = f(t), taking this equation and differentiating it, I get: d2 i(t)/dt2 + 3di(t)/dt + 2i(t) = -e-tu(t). The general form of the equation will be i(t) = in(t) + if(t). Solving for the natural response first: d2 i(t)/dt2 + 3di(t)/dt + 2i(t) = 0, Δ(s) = s2 + 3s + 2 = 0 = (s+1)(s+2) so, in(t) = Ae-t + Be-2t for t>0.
So, at this point I need to solve for the forced response using the original equation I found, I don't know exactly how to do that: d2 i(t)/dt2 + 3di(t)/dt + 2i(t) = -e-tu(t).
I have two questions: #1 is it possible to write a differential equation right off the bat which includes y(t)? questions#2 If i am on the right track so far with the above, what is the next step in finding the forced response?
P.S. I know there are much easier ways of solving this but the problem requires that I solve it using this method...