- #1
Aaerion
- 4
- 2
Problem:
In my class, we have been assigned a project where we must implement a shift and add algorithm to a set of xray images. There are 16 xray images of a finger joint taken with a 5 angle increment using a C-arm xray system. The xray images we will be given is from the second citation that I have below. We have to use the shift and add algorithm with these images to obtain cross-section slices through the entire figure so that we can reconstruct a 3D model of the object shown in the xray projections.
All of the work that we do in this project is based upon two research articles:
Z. Kolitsi, G. Panayiotakis, V. Anastassopoulos, A. Scodras, and N. Pallikarakis, “A multiple projection method for digital tomosynthesis,” Med. Phys. http://dx.doi.org/10.1118/1.596822 19, 1045–1050 (1992).
and
S. Li and H. Jiang, “A practical method for three-dimensional reconstruction of joints using C-arm system and shift-and-add algorithm,” Med. Phys. 32, 1491–1499 (2005). http://dx.doi.org/10.1118/1.1915289My understanding of the problem:
The experimental set-up in Li's article is the following:
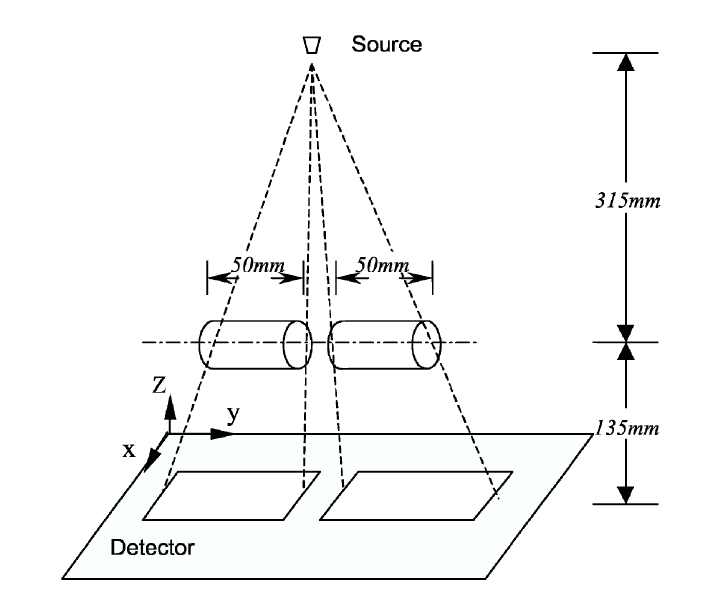
Where the cylindrical object is rotated along the y axis.The variables to describe the shift and add algorithm are given in the below figure:
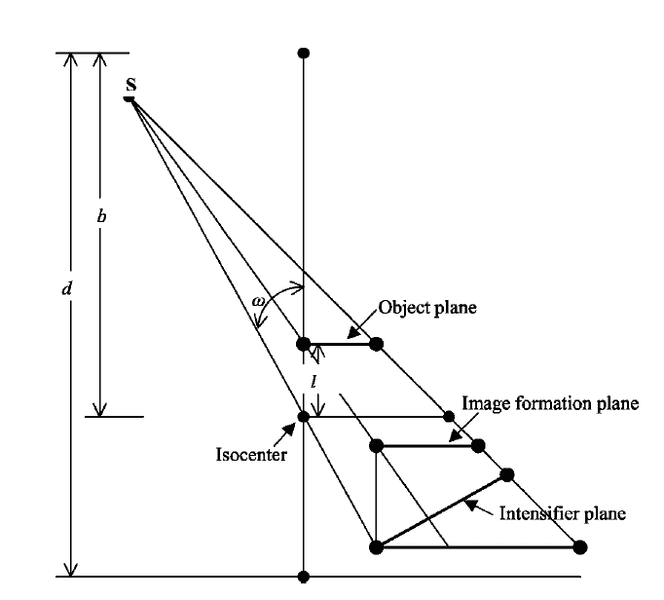
Where:
ω= rotation relative to isocenter
b= distance of source to isocenter
d= distance of source to intensifier plane
l = distance of object plane to isocenter
The given equations in the article to describe the shift-and-add algorithm are the following:

Where:
i = column number in matrix of projection image [tex]M_n(i,j)[/tex]
r= the column position where i is moved to in [tex]M'_n(i,j)[/tex]
The final projection image at depth m is:
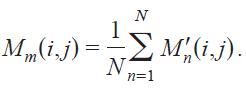
where [tex]M'_n(i,j) = M_n(r,j)[/tex]My attempt:
From the above information, I determined:
i= 1 to total columns of image
l= 0 to 20mm
[tex]\omega= \omega + \Delta \omega = \omega + 5°[/tex]
b= 315 mm
d= 315mm + 135mm =450 mm
I think this might be one place where I am going wrong, but I'm not sure how it would be wrong. The code that I made for this is: http://pastebin.com/S949UbQs
In order to test my code, I followed what Li did in his article and used an xray picture of a cylinder:
http://i1302.photobucket.com/albums/ag122/abysstheory/image1_zpsb2be43fc.jpg
My results looked like this:
http://i1302.photobucket.com/albums/ag122/abysstheory/0_zps21e9ff15.jpeg
http://i1302.photobucket.com/albums/ag122/abysstheory/11_zps0a0c4fe9.jpeg
http://i1302.photobucket.com/albums/ag122/abysstheory/20_zpsd7c1e352.jpeg
When they should have looked like this:
http://i1302.photobucket.com/albums/ag122/abysstheory/Proper_zps41ef5696.pngNoticed Problems:
When I run my code, the value of r is almost always is a non integer value which is strange since it is supposed to be an integer index value. I deal with this by rounding the value of r and using that as the new index value that column i will be shifted to.
Furthermore, I notice that many times r becomes greater than the maximum column value for the matrix or it becomes negative. I currently deal with this in my code by setting r=1, but I'm not sure that this is really the correct way to go about things.
I'm not really sure where I'm going wrong with my implementation of the shift and add algorithm.
In my class, we have been assigned a project where we must implement a shift and add algorithm to a set of xray images. There are 16 xray images of a finger joint taken with a 5 angle increment using a C-arm xray system. The xray images we will be given is from the second citation that I have below. We have to use the shift and add algorithm with these images to obtain cross-section slices through the entire figure so that we can reconstruct a 3D model of the object shown in the xray projections.
All of the work that we do in this project is based upon two research articles:
Z. Kolitsi, G. Panayiotakis, V. Anastassopoulos, A. Scodras, and N. Pallikarakis, “A multiple projection method for digital tomosynthesis,” Med. Phys. http://dx.doi.org/10.1118/1.596822 19, 1045–1050 (1992).
and
S. Li and H. Jiang, “A practical method for three-dimensional reconstruction of joints using C-arm system and shift-and-add algorithm,” Med. Phys. 32, 1491–1499 (2005). http://dx.doi.org/10.1118/1.1915289My understanding of the problem:
The experimental set-up in Li's article is the following:
Where the cylindrical object is rotated along the y axis.The variables to describe the shift and add algorithm are given in the below figure:
Where:
ω= rotation relative to isocenter
b= distance of source to isocenter
d= distance of source to intensifier plane
l = distance of object plane to isocenter
The given equations in the article to describe the shift-and-add algorithm are the following:
Where:
i = column number in matrix of projection image [tex]M_n(i,j)[/tex]
r= the column position where i is moved to in [tex]M'_n(i,j)[/tex]
The final projection image at depth m is:
where [tex]M'_n(i,j) = M_n(r,j)[/tex]My attempt:
From the above information, I determined:
i= 1 to total columns of image
l= 0 to 20mm
[tex]\omega= \omega + \Delta \omega = \omega + 5°[/tex]
b= 315 mm
d= 315mm + 135mm =450 mm
I think this might be one place where I am going wrong, but I'm not sure how it would be wrong. The code that I made for this is: http://pastebin.com/S949UbQs
In order to test my code, I followed what Li did in his article and used an xray picture of a cylinder:
http://i1302.photobucket.com/albums/ag122/abysstheory/image1_zpsb2be43fc.jpg
My results looked like this:
http://i1302.photobucket.com/albums/ag122/abysstheory/0_zps21e9ff15.jpeg
http://i1302.photobucket.com/albums/ag122/abysstheory/11_zps0a0c4fe9.jpeg
http://i1302.photobucket.com/albums/ag122/abysstheory/20_zpsd7c1e352.jpeg
When they should have looked like this:
http://i1302.photobucket.com/albums/ag122/abysstheory/Proper_zps41ef5696.pngNoticed Problems:
When I run my code, the value of r is almost always is a non integer value which is strange since it is supposed to be an integer index value. I deal with this by rounding the value of r and using that as the new index value that column i will be shifted to.
Furthermore, I notice that many times r becomes greater than the maximum column value for the matrix or it becomes negative. I currently deal with this in my code by setting r=1, but I'm not sure that this is really the correct way to go about things.
I'm not really sure where I'm going wrong with my implementation of the shift and add algorithm.