- #1
Saitama
- 4,243
- 93
Homework Statement
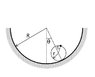
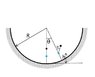
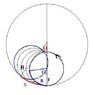
(see attachment for figure)
A small object is mounted to the perimeter of a hoop of radius r. The mass of the object and the hoop is same. The hoop is placed into a fixed semi-cylinder shaped rough trough of radius R, such that small mass is at top. Find the least r/R ratio such that the object performs simple harmonic motion.
Homework Equations
The Attempt at a Solution
I honestly have no idea on how should I begin to solve this problem, this is very different from the SHM problems I have done.
Any help is appreciated. Thanks!
Attachments
Last edited: