- #1
6Stang7
- 212
- 0
I'm trying to determine the centroid of the shape below:

The curve line is that of a circle, but the equation of for a circle, (x-a)2+(y-b)2=r2, won't work here for obvious reasons, but the equation y=r-[tex]\sqrt{2rx-x^{2}}[/tex] does.
To determine the location of the centroid, the formula is:
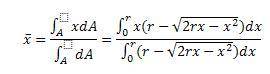
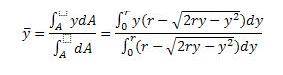
To ensure that the equations that I am using are correct, I am going to compare the area calculated by integrating the line with respect to it's corresponding axis against this equation:
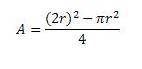
Let's assume that we have a circle with a radius r=1. The area is therefore:
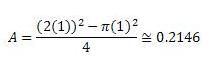
Now, I solved the integral two ways: one with Mathcad, and the other with The Integrator.
When I solve it with Mathcad, I get:

which is wrong because the area calculated is negative. When I solve it with The Integrator, I get:
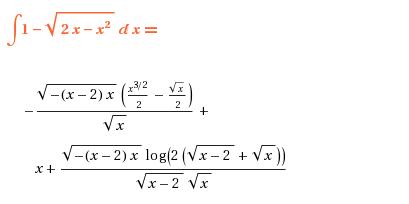
which is also wrong because if this equation where evaluated, you would obtain a number with imaginary components.
I type this equation into my TI-84 and had it calculate the area under the curve and it got an answer that agreed with the known value, so the equation for the curve is correct.
It's been awhile since I've used calculus like this, but this problem should be very straight forward; however, that is not turning out to be the case.
Where have I gone wrong?
EDIT: I'd like to point out that I've already solved for the location of the centroid using a different method. I posted this because I'm more interested in finding out why this method isn't working for me.
The curve line is that of a circle, but the equation of for a circle, (x-a)2+(y-b)2=r2, won't work here for obvious reasons, but the equation y=r-[tex]\sqrt{2rx-x^{2}}[/tex] does.
To determine the location of the centroid, the formula is:
To ensure that the equations that I am using are correct, I am going to compare the area calculated by integrating the line with respect to it's corresponding axis against this equation:
Let's assume that we have a circle with a radius r=1. The area is therefore:
Now, I solved the integral two ways: one with Mathcad, and the other with The Integrator.
When I solve it with Mathcad, I get:
which is wrong because the area calculated is negative. When I solve it with The Integrator, I get:
which is also wrong because if this equation where evaluated, you would obtain a number with imaginary components.
I type this equation into my TI-84 and had it calculate the area under the curve and it got an answer that agreed with the known value, so the equation for the curve is correct.
It's been awhile since I've used calculus like this, but this problem should be very straight forward; however, that is not turning out to be the case.
Where have I gone wrong?
EDIT: I'd like to point out that I've already solved for the location of the centroid using a different method. I posted this because I'm more interested in finding out why this method isn't working for me.
Attachments
Last edited: