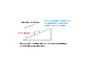
Simple question on direction of friction.

[coreankim]

I was doing some problems, and this thought occurred to me. I've attached the question with the diagrams. Appreciate the help!

 

[Doc Al]

In your second example, the answer is: It depends!

It depends on the force the man is exerting on the block. For example, if he pushes up the incline with a force that just balances the component of weight down the incline, the friction would be zero. No direction whatsoever.

The key is this: Friction always opposes slipping between the surfaces. Look at all the force besides friction that are "trying" to make the object slip along the surface. Friction will oppose that.

(Good question. )

 

[coreankim]

I see! Thanks again.

 

[coreankim]

Actually, that didn't entirely answer my question. Here is the attachment.

 

[Doc Al]

The block doesn't "know" that a man is pushing it. All it "knows" is that there is a net force on it acting down the ramp from all the non-friction forces. This force will tend to make the block slide down the ramp, so friction acts up the ramp to prevent slipping.

Always ask: If there were no friction, which way would the surfaces slide? Friction acts to oppose that sliding.

 

[coreankim]

Friction always points in the direction opposite the net force (excluding friction): this makes intuitive sense. However, this is not always true. For example, let's say that a car that was going up on an inclined plane suddenly breaks. In this case, the only force other than friction that acts on the car is weight, which points down the plane. However, because the car still needs to go some amount up the plane before it stops, friction also points down the plane. The direction of friction and the net force excluding friction point in the same direction.

Am I not accounting for a force, or does friction not always point in the direction opposite the net force?

 

[Doc Al]

Friction always points in the direction opposite the net force (excluding friction): this makes intuitive sense.

That's a useful rule for static situations, not when sliding occurs.

The rule that always works is: Friction acts to oppose slipping between surfaces.

However, this is not always true. For example, let's say that a car that was going up on an inclined plane suddenly breaks. In this case, the only force other than friction that acts on the car is weight, which points down the plane. However, because the car still needs to go some amount up the plane before it stops, friction also points down the plane. The direction of friction and the net force excluding friction point in the same direction.

I'll assume you are talking about a block sliding up an incline (let's not worry about wheels, etc.). So we are talking about kinetic friction, not static. It's easy to find the direction of kinetic friction: As the block slides up, the friction points down; as it slides down, the friction points up.

Let me know if I answered your question.

 

[coreankim]

Ah! That makes perfect sense. Thanks.