- #1
bobsmith76
- 336
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
I don't see how the textbook gets from step 1 to step 2. If anything, the cosines cancel and the answer should be (sine^2)x
bobsmith76 said:Homework Statement
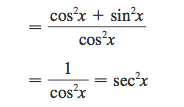
Homework Equations
The Attempt at a Solution
I don't see how the textbook gets from step 1 to step 2. If anything, the cosines cancel and the answer should be (sine^2)x
You pretty much can't simplify trig expressions without having a few identities in mind, so I would advise you to spend some time reviewing them.bobsmith76 said:thanks, trig identities, I forgot about them
A trigonometric expression is a mathematical expression that contains trigonometric functions such as sine, cosine, tangent, and their inverses. These functions involve ratios of the sides of a right triangle and are commonly used in geometry and physics.
Simplifying trigonometric expressions can make them easier to work with and can reveal relationships between different trigonometric functions. It can also help in solving equations and proving identities.
The steps to simplify a trigonometric expression include:
1. Use trigonometric identities to rewrite the expression
2. Simplify any complex fractions
3. Combine like terms
4. Use the unit circle or special triangles to simplify any trigonometric functions
5. Check your answer by plugging in values to the original expression.
No, not all trigonometric expressions can be simplified. Some expressions may already be in their simplest form, while others may not have any known identities or simplifications.
Some common mistakes when simplifying trigonometric expressions include:
- Not using the correct trigonometric identities
- Forgetting to simplify complex fractions
- Incorrectly combining like terms
- Making calculation errors
It is important to double-check your work and use a calculator or reference guide when needed.