Single phase induction motor

[cnh1995]

Single phase motor is not self starting, so it is started using some arrangement and the starting arrangement is disconnected(not always) once the motor is set in proper motion(about 70% of the maximum speed).

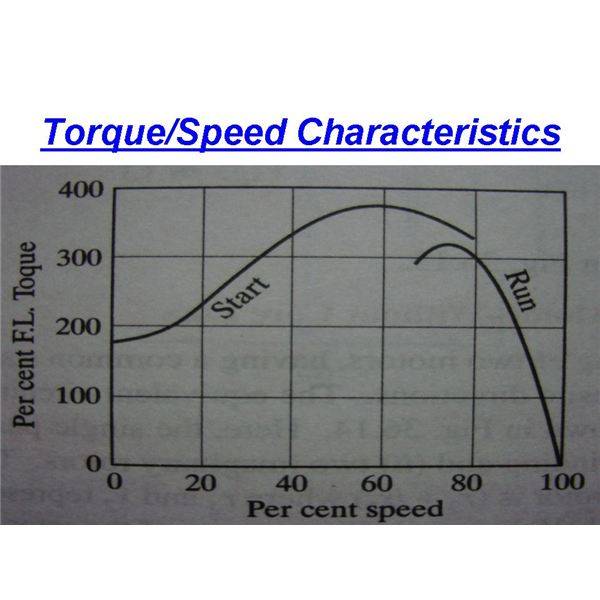
But I didn't understand this graph. From the starting moment, motor accelerates and catches speed. This must reduce the slip. So, the torque should go on decreasing as the speed goes up. Then why is the torque curve in the graph shown rising from the starting instant? Have I overlooked something?

 

[Averagesupernova]

The torque increases as rotor speed increases because the frequency of the rotor currents decrease as the speed comes up. The inductive reactance of the rotor prevents higher currents at low RPM (higher frequency currents).

 

[Babadag]

In the unstable zone if the load increases the acceleration torque will be negative that means will brake the motor reducing the speed. Less speed=less torque and the motor will decelerate further until stops.

In the stable zone if the load increases the acceleration torque will be negative for now ,that means will brake the motor reducing the speed. Less speed=more motor torque in this region.

The motor torque increases until will equal the load torque.The motor will rotate at this new

slip stable.

 

[anorlunda]

Nautical "to make fast" means to attach securely. You got it.

 

[cnh1995]

In the unstable zone if the load increases the acceleration torque will be negative that means will brake the motor reducing the speed. Less speed=less torque and the motor will decelerate further until stops.

In the stable zone if the load increases the acceleration torque will be negative for now ,that means will brake the motor reducing the speed. Less speed=more motor torque in this region.

The motor torque increases until will equal the load torque.The motor will rotate at this new

slip stable.

If I started the motor at no load, its final speed will be close to the synchronous speed and final torque will be almost 0. But at the starting instant, there will be a finite starting torque(regardless of the load). So, the torque will go on decreasing as the motor accelerates, from starting torque Ts to 0 torque, right? What would that graph look like?

 

[jim hardy]

If I started the motor at no load, its final speed will be close to the synchronous speed and final torque will be almost 0. But at the starting instant, there will be a finite starting torque(regardless of the load).

of course. But i think you are not quite completely thinking through what happens to torque as the motor starts.
Torque developed by the motor doesn't all go into driving an external mechanical load, much of it must go into accelerating the motor plus its external load. So what you measure at the shaft must be corrected for dω/dt and total moment of inertia.

Have you ever listened while a motor starts a high inertia load like a bench grinder with two big heavy wheels??
You'll hear it hum and accelerate slowly until speed approaches that peak region
then speed almost snaps up that last few hundred RPM to near synchronous.
That to me is the a beautiful demonstration of the effect Mr Av'supernova described. Surely a friend has an old fashioned bench grinder where you could experiment. Grind on something and feel how steep is the Right-hand slope of that speed/torque curve. Then force it past peak and feel how easily you can grind_{oohh terrible pun-sorry} it to a halt.

So, the torque will go on decreasing as the motor accelerates, from starting torque Ts to 0 torque, right? What would that graph look like?

in most motors torque increases until peak, decreases thereafter because of ratio of rotor resistance to inductance.
Remember a lot of torque goes into accelerating the rotating inertia
so to measure it you'd have to use a brake and hold speed constant at each data point.

Designers can build the rotor to give custom speed-torque curves by adjusting size & shape shape of rotor bars to tweak their resistance and moving them deeper into the iron to tweak their inductance.
you'd want an A curve motor for a bench grinder because it'd really hang in there when you get aggressive on a workpiece
and a D curve for an elevator because its curve has no cusp - only sudden change of acceleration will be at start and stop giving a perceived smoother ride.. no'jerk'

this is a nice page to peruse, that 'typical' curve set just above came from it.
http://ecmweb.com/motors/understanding-induction-motor-nameplate-information

in my motors class (1965) we had an induction motor with wound rotor and brushes. That let us use an external rotor resistor so we could run it any class, and did such experiments. I hope such labs still exist for undergrads. I visited my Alma Mater a couple months ago, walking through that lab was nostalgic but my goodness how the electronics has taken over motor drives!

old jim

 

[cnh1995]

of course. But i think you are not quite completely thinking through what happens to torque as the motor starts.
Torque developed by the motor doesn't all go into driving an external mechanical load, much of it must go into accelerating the motor plus its external load. So what you measure at the shaft must be corrected for dω/dt and total moment of inertia.

Have you ever listened while a motor starts a high inertia load like a bench grinder with two big heavy wheels??
You'll hear it hum and accelerate slowly until speed approaches that peak region
then speed almost snaps up that last few hundred RPM to near synchronous.
That to me is the a beautiful demonstration of the effect Mr Av'supernova described. Surely a friend has an old fashioned bench grinder where you could experiment. Grind on something and feel how steep is the Right-hand slope of that speed/torque curve. Then force it past peak and feel how easily you can grind_{oohh terrible pun-sorry} it to a halt.

in most motors torque increases until peak, decreases thereafter because of ratio of rotor resistance to inductance.
Remember a lot of torque goes into accelerating the rotating inertia
so to measure it you'd have to use a brake and hold speed constant at each data point.

Designers can build the rotor to give custom speed-torque curves by adjusting size & shape shape of rotor bars to tweak their resistance and moving them deeper into the iron to tweak their inductance.
you'd want an A curve motor for a bench grinder because it'd really hang in there when you get aggressive on a workpiece
and a D curve for an elevator because its curve has no cusp - only sudden change of acceleration will be at start and stop giving a perceived smoother ride.. no'jerk'

this is a nice page to peruse, that 'typical' curve set just above came from it.
http://ecmweb.com/motors/understanding-induction-motor-nameplate-information

in my motors class (1965) we had an induction motor with wound rotor and brushes. That let us use an external rotor resistor so we could run it any class, and did such experiments. I hope such labs still exist for undergrads. I visited my Alma Mater a couple months ago, walking through that lab was nostalgic but my goodness how the electronics has taken over motor drives!

old jim

Thanks a lot! That was very helpful. Its great to see your unique and classic style of explanation once again !

 

[jim hardy]

oh my goodness- thanks for the kind words. Helps an old guy feel a teeny bit useful.

Glad it helped.

 

[Babadag]

I think I am late. However, you said:

“the torque will go on decreasing as the motor accelerates, from starting torque Ts to 0 torque, right?”

It is not entirely right. At the beginning the torque increases as motor accelerate up to maximum torque. From here up to rated –or no-load-speed will decrease.

The rotor current will be:

I2=E2/sqrt(R2^2+X2^2) E2=E2o*s X2=X2o*s where:

R2=rotor resistance E2=EMF at slip s E2o= EMF at locked rotor X2o rotor reactance at locked[stand still] rotor.

Pi =transferred power from stator through gap.

Pi=m2*R2/s*I2^2

where m2 is the rotor phase number.

The torque it is:

Pi/w where w=2*pi*ns ns=synchronous speed in rps[rotation per seconds]

Let’s say krs=rotor turns/phase/stator turns/phase [if winding factor would be 1].

Then E2o/E1= krs and if E1~V then

I2=V*s/sqrt(R2^2+X2o^2*s^2)* krs
and if we take K=m2^2*V^2*krs^2/w then

T=K*R2*s/(R2^2+Xo^2*s^2) s=1 Tst=K*R2/(R2^2+Xo^2)

If dT/ds=0 we shall get Tmaxim [sk for Tmaxim].

sk=+/-R2/X2o [+ for motor stage – for generator].

However, we neglected skin effect which may alter the equation a bit but for general information

it works.

Let’s say srated=0.05 and sk=1/3=0.33- as usually.

Then R2=1 and X2o=3

s=1 Tst=K/(1+9)=K/10=0.1K

s=0.5 T =K*0.5/(1+9*.25)=0.154K

sk=0.33 Tmax=K*.033/(1+1)=0.165K

s=0.05 Trated=0.05*K/(1+0.05^2*9)=0.0489K

You can see up to sk the torque increases when slip decreases. After then the torque decrease if

the slip decreases.

 

[cnh1995]

I think I am late. However, you said:

“the torque will go on decreasing as the motor accelerates, from starting torque Ts to 0 torque, right?”

It is not entirely right. At the beginning the torque increases as motor accelerate up to maximum torque. From here up to rated –or no-load-speed will decrease.

The rotor current will be:

I2=E2/sqrt(R2^2+X2^2) E2=E2o*s X2=X2o*s where:

R2=rotor resistance E2=EMF at slip s E2o= EMF at locked rotor X2o rotor reactance at locked[stand still] rotor.

Pi =transferred power from stator through gap.

Pi=m2*R2/s*I2^2

where m2 is the rotor phase number.

The torque it is:

Pi/w where w=2*pi*ns ns=synchronous speed in rps[rotation per seconds]

Let’s say krs=rotor turns/phase/stator turns/phase [if winding factor would be 1].

Then E2o/E1= krs and if E1~V then

I2=V*s/sqrt(R2^2+X2o^2*s^2)* krs
and if we take K=m2^2*V^2*krs^2/w then

T=K*R2*s/(R2^2+Xo^2*s^2) s=1 Tst=K*R2/(R2^2+Xo^2)

If dT/ds=0 we shall get Tmaxim [sk for Tmaxim].

sk=+/-R2/X2o [+ for motor stage – for generator].

However, we neglected skin effect which may alter the equation a bit but for general information

it works.

Let’s say srated=0.05 and sk=1/3=0.33- as usually.

Then R2=1 and X2o=3

s=1 Tst=K/(1+9)=K/10=0.1K

s=0.5 T =K*0.5/(1+9*.25)=0.154K

sk=0.33 Tmax=K*.033/(1+1)=0.165K

s=0.05 Trated=0.05*K/(1+0.05^2*9)=0.0489K

You can see up to sk the torque increases when slip decreases. After then the torque decrease if

the slip decreases.

Thanks. This will help me understand this behavior mathematically.