Solve Rod Slider Energy Problem: Find Velocities of Collar B

[stinlin]

Homework Statement

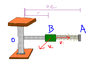
Collar B has a mass of 4 kg and is attached to a spring of constant 1500 N/m and of undeformed length 0.4 m. The system is set in motion with r = 0.2 m, v_theta = 6 m/s, and v_r = 0. Neglecting the mass of the rod and the effect of friction, determine the radial and transverse components of the velocity of the collar when r = 0.5 m.


2. Relevant theories

Conservation of energy - kinetic and potential energy

The Attempt at a Solution

I used conservation of energy :

V_spring_initial = V_spring_final + T_slider_final

x_initial_spring = abs(0.2-0.4)
x_final_spring = abs(0.5-0.4)


I solved for v_r and got 3.35 m/s, which is NOT the right answer.

If I figure out how to solve for v_r, I'm still in the situation where I don't really know how to solve for v_theta. I'm thinking I can determine the force due to the spring and set that equal to m*a_normal, solve for v_theta there (because v^2 = (v_tangential)^2 = (v_theta)^2).

Can I get some help? Thanks a bunch!

 

[Saketh]

Use conservation of angular momentum to find the velocity in the tangential direction as a function of the radius.

Use a net force equation to find the velocity in the radial direction as a function of the radius. (You can consider it as an "inertial" frame with a fictional force, if you want.)

 

[stinlin]

We haven't done angular momentum in class yet. While I do know it, he wants us to try and stick to the concepts we know.

 

[stinlin]

Is there any more thoughts on this one or no??

 

[andrevdh]

If one looks at just the SHM motion of the slider its energy stays constant throughout the motion:

$$\frac{1}{2}Ax^2$$

which enables one to calculate the radial velocity at any position.

Looking at the bigger picture the total mechanical energy (which will stay
constant since the slider is subject to a conservative force) of the slider should also include its rotational kinetic energy:

$$\frac{1}{2}I\omega ^2$$

, where its rotational velocity is determined by the tangential velocity.

 

[stinlin]

But the concept of moment of inertia hasn't been formally introduced in our class yet, so we can't really use that equation.

 

[cipotilla]

How did you get the answer for Vr? What principle did you use? I was going to suggest you use the work-energy principle.

 

[andrevdh]

But the concept of moment of inertia hasn't been formally introduced in our class yet, so we can't really use that equation.

Ok. You can then still use the fact that T + V will stay constant. The speed that you get will be the real speed of the slider, that is the tangential and radial speed combined or just v.