Snell's Law in birefringent materials

[bayners123]

Homework Statement

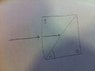
I'm trying to work out what happens why light hits a boundary between two birefringent materials with their optical axis perpendicular. It's hard to describe so I've attached a diagram. The upper wedge has an optical axis pointing upwards, the lower wedge has it coming out of the page.

Snell's equation is $$sin(\theta_T) = \frac{n_1}{n_2} sin(\theta_i)$$
For linearly polarized light out of the plane of reflection (s polarization) $$n_1 = n_o$$ and $$n_2 = n_e$$ (both slabs are made of the same material with different orientations).
For light polarized in the plane though I'm confused: as it comes in the light oscillates in the optical axis but once it is reflected it oscillates perpendicular to it. What should I take for n1?

Also, the question asks for ray diagrams in the case of a) planar polarization b) perpendicular polarization c) circular polarization and d) unpolarized light. I've discussed a) and b), but am I right in thinking that c) and d) are just both rays happening at once with half the intensity?

Homework Equations

$$sin(\theta_T) = \frac{n_1}{n_2} sin(\theta_i)$$

The Attempt at a Solution

 

[jbsteele]

For planar polarization, I believe n_1 is just the ordinary refractive index, since the light oscillates parallel to the optical axis. For perpendicular polarization, I think n_1 should be the extraordinary refractive index, since the light oscillates in the opposite direction. For circular polarization, I think it is just both rays happening at once with half the intensity. For unpolarized light, I think it is the same as circular polarization, but with equal intensities for each ray.