- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- See attached
- Relevant Equations
- understanding of integration and separation of variables.
This is the question;
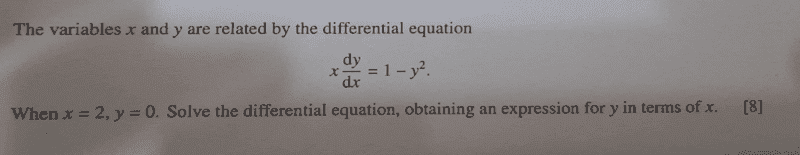 This is the solution;
This is the solution;

Find my approach here,
##x####\frac {dy}{dx}##=##1-y^2##
→##\frac {dx}{x}##=##\frac {dy}{1-y^2}##
I let ##u=1-y^2## → ##du=-2ydy##, therefore;
##\int ####\frac {dx}{x}##=##\int ####\frac {du}{-2yu}##, we know that ##y##=##\sqrt {1-u}##
##\int ####\frac {dx}{x}##=##\int ####\frac {du}{-2u\sqrt {1-u}}## i let,
##\frac {1}{u\sqrt {1-u}}##=##\frac {A}{\sqrt {1-u}}##+##\frac {B}{u}##
→##1=##Au##+##B##\sqrt {1-u}##
##A=0.5## and ##B=0.5## * i need to check how to arrive at this...i got a bit stuck here...
Therefore,
##\frac {1}{-2}##[##\int####\frac {0.5}{\sqrt {1-u}}####du##+##\int####\frac {0.5}{u}]####du##=##\int ####\frac {dx}{x}##
##\frac {1}{-4}####\int####\frac {1}{\sqrt {1-u}}####du##+##\frac {1}{-4}####\int####\frac {1}{u}####du##=##\int ####\frac {dx}{x}##
on integration we shall have,
##-0.25(1-(1-y^2))-0.25 ln|1-y^2|##=##ln|x|## + ##k##
##-0.25y^2-0.25ln|1-y^2|##=##ln|x|## + ##k##
using and applying the initial conditions ##y(2)=0##, we get,
##k=-ln2##
i will need to re check this later...something does not look right...i will amend this post to correct solution then look at the suggested approach...
Find my approach here,
##x####\frac {dy}{dx}##=##1-y^2##
→##\frac {dx}{x}##=##\frac {dy}{1-y^2}##
I let ##u=1-y^2## → ##du=-2ydy##, therefore;
##\int ####\frac {dx}{x}##=##\int ####\frac {du}{-2yu}##, we know that ##y##=##\sqrt {1-u}##
##\int ####\frac {dx}{x}##=##\int ####\frac {du}{-2u\sqrt {1-u}}## i let,
##\frac {1}{u\sqrt {1-u}}##=##\frac {A}{\sqrt {1-u}}##+##\frac {B}{u}##
→##1=##Au##+##B##\sqrt {1-u}##
##A=0.5## and ##B=0.5## * i need to check how to arrive at this...i got a bit stuck here...
Therefore,
##\frac {1}{-2}##[##\int####\frac {0.5}{\sqrt {1-u}}####du##+##\int####\frac {0.5}{u}]####du##=##\int ####\frac {dx}{x}##
##\frac {1}{-4}####\int####\frac {1}{\sqrt {1-u}}####du##+##\frac {1}{-4}####\int####\frac {1}{u}####du##=##\int ####\frac {dx}{x}##
on integration we shall have,
##-0.25(1-(1-y^2))-0.25 ln|1-y^2|##=##ln|x|## + ##k##
##-0.25y^2-0.25ln|1-y^2|##=##ln|x|## + ##k##
using and applying the initial conditions ##y(2)=0##, we get,
##k=-ln2##
i will need to re check this later...something does not look right...i will amend this post to correct solution then look at the suggested approach...
Last edited:


 Bingo !
Bingo !