Solve Magnetic Field from Perpendicular Wires Carrying Same Current

[NotaPhysicsMan]

Ok, since I got little feedback, I will try it again, but please help. It's due tomorrow!

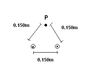
The drawing (attachment) shows two wires that carry the same current of I=85.0 A are are oriented perpendicular to the plane of the paper. The current in one wire is directed out of the paper, while the current in the other is directed into the paper. Find the magnitude and direction of thenet magnetic field at point P.

For those who can't get the attacment, the drawing is simple:

    P

X       0

A equilateral triangle with sides of 0.150 m, X being current into and 0 being out of.

Ok it seems that I just have to use: B=uI/2pieR to get the magnitude of the diagonal.

Using the right hand rules I draw two circlular fields reaching point P sort of like venn diagrams. Ok the radius is really just the distance from the currents to the P, so R=0.150m.

B=4pie x 10^-7 (85.0A)/ 2pie (0.150m)
B=1.133x10^-4 T.

Next:

I have two right angle triangles split in half, with the x-directions cancelling each other and the y-direction adding together going downwards. Ok so each of the angles will give 60/2=30. So 1.133x10^-4 T(cos30)=9.812x10^-5T for the y and for x=5.665x10^-5 T. X's will cancel. And for Y's or the net magnetic field is:

(2 x 9.812x10^-5T)=1.96x10^-4 T downwards?

Ok 1 other thing my friend did was just use cos 60 instead of cos 30. The answer comes out to be 1.133x10^-4, which is in fact correct according to my teacher. BUT why would you use 60 degrees. It's an equilateral triangle but you can't just you the right triangle relationships unless you split the triangle up into halves, in which case you would have 30 degrees each... :yuck:

 

[Andrew Mason]

A equilateral triangle with sides of 0.150 m, X being current into and 0 being out of.

Ok it seems that I just have to use: B=uI/2pieR to get the magnitude of the diagonal.

You are substituting values too early and obcsuring the physics. Work it out algebraically and plug in the values at the end.

$$\vec B = \frac{\mu_0I}{2\pi R} \hat I \times \hat r$$

So at P the field B from the left wire is 90 deg to the radius so it makes a 60 deg angle to the vertical. Its vertical component is Bcos(60). The same for the wire from the right. The horizontal components are Bsin(60) (right) and Bsin(60)(left) so they cancel.

$$B_P = 2Bcos(60) = 2\frac{\mu_0I}{2\pi R}(.5) = \frac{\mu_0I}{2\pi R}$$

AM

 

[NotaPhysicsMan]

Darn, I screwed up the degrees...ok 60 is right. Thanks.