Source-free current response

[k_squared]

1. Homework Statement
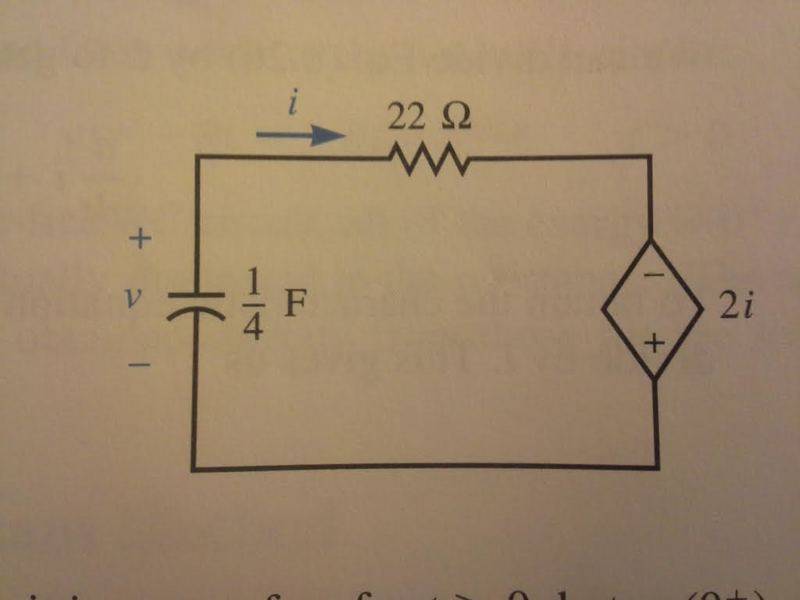
For the following circuit, use KVL to write a differential equation in terms of current i and solve for the source-free current response if v(0+) = 40 V.

Homework Equations

$$(s-s_1)Ae^{st}=0$$
$$i=C(d/dt)v$$
$$v=Ae^{s_1*t}$$

$$i=(-1/R)V_0e^{\frac{-t/}{RC}}$$

The Attempt at a Solution

[/B]
Finding the initial current is not so difficult. We have: $$-40 +22i-2i=0$$, for an initial current of 2 amps.

I came up with: $$(4)i-22(d/dt)i+2(d/dt)i=0$$, thus with 4/24, we have $$s+1/6=0$$.

However the answer is $$2e^{-\frac{1}{5}t}$$, meaning that s_1= 1\5, not 1\6!

I assume the two and the four have to be the same sign, because they are both voltage sources that are lined up with each other such that their voltage becomes greater rather than lesser. However, this means that s_1 becomes positive, or the sources of voltage in this circuit (ie, the capacitor and the dependent voltage source) have different signs!

Alas, s_1 is negative as expected. Therefore, I must be missing something.

What am I doing wrong?

 

[k_squared]

Wait... is it because any component with $$d/dt$$ is going to be negative in a stable circuit?

 

[rude man]

1. Homework Statement

I came up with: $$(4)i-22(d/dt)i+2(d/dt)i=0$$, thus with 4/24, we have $$s+1/6=0$$.

Not sure I understood everything you wrote, but your equation here has the wrong polarities.
I also don't follow how you solved your diff. eq.

 

[NascentOxygen]

I came up with:

​

(4)i-22(d/dt)i+2(d/dt)i=0

I think this simplifies to
(4)i - 20(d/dt)i = 0
so there's your 5.

But haven't you inadvertently swapped i where you should have v here?

 

[rezeew]

Dear student,

Thank you for sharing your attempt at solving this problem. Your approach seems reasonable, but there are a few things that you may have overlooked or misunderstood.

Firstly, your initial current calculation is incorrect. The voltage across the 22Ω resistor is -40V, not +40V as you have assumed. This is because the current is flowing in the opposite direction of the voltage drop. Therefore, the correct equation should be: -40V + 22i + 2i = 0, giving an initial current of -2A.

Secondly, your differential equation is also incorrect. The correct form should be: -40V + 22i + 2i = -20i = 0, since there is no voltage source in the circuit and the dependent voltage source is multiplied by the current. Solving for i, we get i = 0, meaning there is no current in the circuit.

Finally, the answer given in the problem, 2e^(-1/5t), is the correct solution. This can be obtained by solving the differential equation: -20(di/dt) = 0, giving di/dt = 0. Integrating both sides with respect to time, we get i = 2e^(-1/5t) + C, where C is the constant of integration. Since the initial current is 0, C = 0 and we are left with the final solution of i = 2e^(-1/5t).

I hope this clears up any confusion and helps you understand the problem better. Keep up the good work!

Best regards,