- #1
dwn
- 165
- 2
Homework Statement
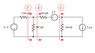
Image Attached
Homework Equations
Ohm's
The Attempt at a Solution
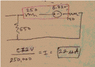
Combined the two resistors in series : 250 + 550 = 800 kΩ
Source Transformation (Current Source): V = 140,000(2*10^-6)= 0.28 V
Combine the voltage sources : 6 - 0.28 = 5.72 V
But then I recreated the circuit with these figures and it just doesn't appear correct to me.
Voltage source = 5.72 V
Resistor = 800 + 140 = 940kΩ
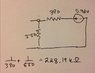
Ans: V = 3.35 V R = 228.19 kΩ
I don't see how they're getting these figures.