Solving Unexpected Integral Problem with Bessel Functions

[sukharef]

Hello!
I've got unexpected problems with this very integral.

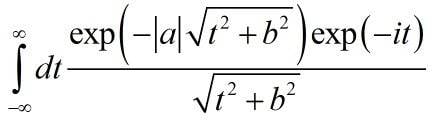
I've looked through "gradshteyn and ryzhik" and found similar, but not the same. So the result, as i think, will be Bessel functions or so. Wolfram Mathematica could not calculate it, so i thought you would help with it, because it does not seem to be very difficult.

Thank you in advance!

 

[RUber]

I'm interested to hear what you are working on.
I have dealt with that specific integral myself and found a reference showing that it is equivalent to
$\pi \mathrm{i} H_0^1 ( \mathrm{i} b |a| )$ or $2K_0 (b |a| ).$
The constants may be off...but I am pretty sure about the result.
Duran, Muga, and Nedelec use a transformation in "The Helmholtz equation in a locally perturbed half-plane with passive boundary." IMA Jrnl. of Appl. Math. 2006.
Which fits the forms you will find in Gradshteyn and Ryzhik.
This method was used by Van and Wood in, "A Time-Domain Finite Element Method for Helmholtz Equations." Jrnl. of Comp. Phys. 2002.
I hope this is helpful...I could not actually do the transformations myself, so I had to rely on some smart folks who had done it before me.

 

[sukharef]

I'm interested to hear what you are working on.
I have dealt with that specific integral myself and found a reference showing that it is equivalent to
$\pi \mathrm{i} H_0^1 ( \mathrm{i} b |a| )$ or $2K_0 (b |a| ).$
The constants may be off...but I am pretty sure about the result.
Duran, Muga, and Nedelec use a transformation in "The Helmholtz equation in a locally perturbed half-plane with passive boundary." IMA Jrnl. of Appl. Math. 2006.
Which fits the forms you will find in Gradshteyn and Ryzhik.
This method was used by Van and Wood in, "A Time-Domain Finite Element Method for Helmholtz Equations." Jrnl. of Comp. Phys. 2002.
I hope this is helpful...I could not actually do the transformations myself, so I had to rely on some smart folks who had done it before me.

Thank you!
I'm trying to calculate radiation arises when a particle moves along the shaped surface.
I've looked through the articles and i want to know what transformation do you exactly mean, specific polar coordinates?
I guess if the result would be πiH10(ib|a|) or 2K0(b|a|) Wolf.Mathematica would calculate it in terms of these functions. Maybe it's not that simple.

 

[RUber]

The explanation of the parametrization is in the Duran article.

 

[sukharef]

The explanation of the parametrization is in the Duran article.
View attachment 87518

are you sure about the title of the article? i can not find that piece that you are referring to.
besides the integral (10) has a singularity on Re axis, not on I am like mine one has.

 

[SteamKing]

are you sure about the title of the article? i can not find that piece that you are referring to.
besides the integral (10) has a singularity on Re axis, not on I am like mine one has.

I think the paper in Ref. 5 here:

http://cib.epfl.ch/Rappaz60/programme/JeanClaudeNedelec.pdf

and

http://imamat.oxfordjournals.org/content/71/6/853.abstract

is the paper referred to by RUber above, I believe.

 

[sukharef]

I think the paper in Ref. 5 here:

http://cib.epfl.ch/Rappaz60/programme/JeanClaudeNedelec.pdf

and

http://imamat.oxfordjournals.org/content/71/6/853.abstract

is the paper referred to by RUber above, I believe.

Thank you, wrong paper i was looking through.

 

[RUber]

In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be $\sqrt{a^2 + 1}$ k= -ib.
So, would $iH_0^1(ib\sqrt{a^2 + 1})$ work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?

 

[sukharef]

In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be $\sqrt{a^2 + 1}$ k= -ib.
So, would $iH_0^1(ib\sqrt{a^2 + 1})$ work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?

no, b and a are real. i meant that k = +-ib.

 

[sukharef]

In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be $\sqrt{a^2 + 1}$ k= -ib.
So, would $iH_0^1(ib\sqrt{a^2 + 1})$ work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?

i think 2K0() is more appropriate here, because in particular case of a=0, the result will be 2K0(b)