- #1
Loren Booda
- 3,125
- 4
How many cubes of side 1 centimeter can fit into a sphere of diameter 3 centimeters?
Mark44 said:I'll say 8.
Since the volume of such a sphere is ~ 9.42 cm3, no more than 9 unbroken cubes could possibly fit into this sphere
Dickfore said:I would say 6.
DaveC426913 said:Arranged how?
Dickfore said:Imagine a cube with all vertices on one of its side touching the sphere. The height of the spherical cap cut by the opposite side of the cube is:
Therefore, we cannot accommodate a single extra cube in this internal cube.
DaveC426913 said:Uh. OK. So arranged how? You said six cubes. How do you see them being arranged?
Dickfore said:Imagine a Cartesian coordinate system. It cuts the sphere at six points. You place the cubes "near" these points.
DaveC426913 said:Still having trouble.
1] Seems to me it would cut the sphere via planes, not points.
2] Do these 6 cubes touch each other?
Oh, I think I see. We're all building a mass of cubes glued together in the middle. You're attaching the cubes to the inside surface of the sphere. So, they touch the sphere at 6 equidistant points. They may or may not touch each other.
Right.Dickfore said:Ahh:
They will block each other. In this way, I will only be able to put 2.
DaveC426913 said:I say 4, arranged tetrahedrally.
Mark44 said:I'll say 8.
Since the volume of such a sphere is ~ 9.42 cm3, no more than 9 unbroken cubes could possibly fit into this sphere
Loren Booda said:How many cubes of side 1 centimeter can fit into a sphere of diameter 3 centimeters?
Dickfore said:There can definitely be 4 cubes. Just order them to form a square prism with side 2 and height 1. Here is the relevant diagram.
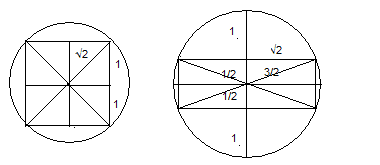
tauon said:can you upload that image to imageshack or something? I'd like to see it and it's saying "pending attachment aproval" on my end... :(
Loren Booda said:My guess is that the tetrahedron, if it fits, would be asymmetric. Please describe your array.
A rotation for a 1x2 refers to the movement of the two-dimensional shape in a circular motion around a fixed point, such as its center or a designated pivot point.
There is no limit to the number of rotations a 1x2 can have. As long as the shape remains within the boundaries of the sphere and does not overlap with itself, it can rotate infinitely.
Yes, a 1x2 can be rotated in any direction within the sphere as long as it does not intersect with itself or exceed the boundaries of the sphere.
There are an infinite number of unique ways a 1x2 can be rotated in a sphere. Each rotation may have a slightly different orientation or position within the sphere, making it unique.
The only limitation to how a 1x2 can be rotated in a sphere is that it cannot intersect with itself or exceed the boundaries of the sphere. Other than that, it can rotate in any direction and orientation.